题目内容
1.已知a≥0,b≥0,求证:a6+b6≥ab(a4+b4).分析 利用作差法,通过分类讨论判断即可.
解答 证明:a6+b6-ab(a4+b4)=(a-b)(a5-b5),
当a≥b≥0时,a5≥b5,a-b≥0,a5-b5≥0,可得(a-b)(a5-b5)≥0.所以a6+b6≥ab(a4+b4).
当0≤a<b时,a5<b5,a-b<0,a5-b5<0,可得(a-b)(a5-b5)>0.所以a6+b6>ab(a4+b4).
综上a≥0,b≥0,a6+b6≥ab(a4+b4).
点评 本题考查不等式的证明,考查分类讨论,作差法的应用,是中档题.

练习册系列答案
相关题目
12.设集合M={x|log2(x-1)>0},集合N={x|x≥-2},则N∩∁RM=( )
| A. | {x|x≤-2} | B. | {x|-2<x≤2} | C. | {x|-2≤x≤3} | D. | {x|-2≤x≤2} |
16.在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点.若异面直线PA与BE所成的角为45°,则四棱锥的体积是( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
6.执行如图所示的程序框图,则输出的结果是( )
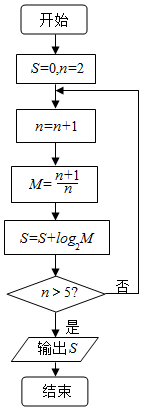

| A. | 1 | B. | log2$\frac{6}{5}$ | C. | log2$\frac{7}{3}$ | D. | log23 |
13.若sin(θ-$\frac{π}{3}$)=$\frac{1}{3}$,0<θ<π,则cosθ=( )
| A. | $\frac{-\sqrt{3}+2\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}+2\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{3}±2\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}±2\sqrt{2}}{6}$ |