题目内容
16.在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点.若异面直线PA与BE所成的角为45°,则四棱锥的体积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 设底面ABCD的中心为O,PC中点为E,则∠BEO为异面直线PA与BE所成的角,于是OE=OB=1,从而求出棱锥的底面边长和棱锥的高.
解答  解:设底面ABCD的中心为O,PC中点为E,连结AC,OE,OB,PO.
解:设底面ABCD的中心为O,PC中点为E,连结AC,OE,OB,PO.
则OE∥PA,OE=$\frac{1}{2}$PA=1.
∴∠BEO为异面直线PA与BE所成的角,即∠BEO=45°.
∵四边形ABCD是正方形,∴BO⊥AC.
∵PO⊥OB,PO∩AC=O,
∴BO⊥平面PAC,∵OE?平面PAC,
∴OB⊥OE,
∴△BOE是等腰直角三角形,
∴OB=OE=1,
∴PO=$\sqrt{P{B}^{2}-O{B}^{2}}=\sqrt{3}$,BC=$\sqrt{2}$.
∴四棱锥的体积V=$\frac{1}{3}×(\sqrt{2})^{2}×\sqrt{3}=\frac{2\sqrt{3}}{3}$.
故选D.
点评 本题考查了棱锥的结构特征,空间角的作法,体积计算,属于中档题.

练习册系列答案
相关题目
7.按顺序输入x,y,z的值,运行如图的程序后,输出的结果为8,则输入的x,y,z的值可能是( )
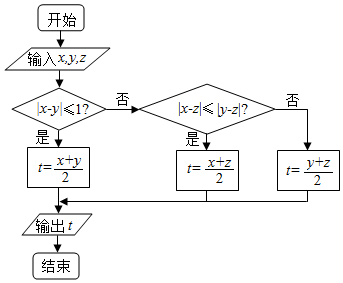

| A. | x=6,y=8,z=9 | B. | x=8,y=7,z=9 | C. | x=8,y=6,z=10 | D. | x=8,y=6,z=8 |
4.设实数x、y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{3x-y-3≤0}\end{array}\right.$,则z=|x-4y+1|的最大值和最小值之和是( )
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
11.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( )
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
8.已知函数f(x)=x3-x2-x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
5.已知函数f(x)=cos2x+asinx在区间(0,nπ)内恰有8个零点,则实数a的取值范围与最小正整数n的值分别为( )
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |