题目内容
求函数y=3sin（2x+
）的最大值和最小值及相应的x值的范围．
| π |
| 3 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据正弦函数的定义域和值域，求得y=3sin（2x+
）的最大值和最小值及相应的x值．
| π |
| 3 |
解答：
解：对于函数y=3sin（2x+
），
当2x+
=2kπ+
，k∈z时，即x=kπ+
时，函数y取得最大值为3，
当2x+
=2kπ-
，k∈z时，即x=kπ-
时，函数y取得最小值为-3．
| π |
| 3 |
当2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
当2x+
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评：本题主要考查利用y=Asin（ωx+φ）的图象特征，正弦函数的定义域和值域，属于中档题．
练习册系列答案
相关题目
若复数z满足z（2-i）=1，则
=（ ）
. |
| z |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
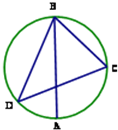圆形广场的有南北两个大门在中轴线上，东、西各有一栋建筑物与北门的距离分别为30米和40米，且以北门为顶点（视大门和建筑物为点）的角为60°，求广场的直径（保留两位小数）．