题目内容
11.在等差数列中,S17=34,则a2+a16等于( )| A. | 17 | B. | 6 | C. | 4 | D. | 2 |
分析 由等差数列的性质可得:a2+a16=a1+a17.再利用等差数列的前n项和公式即可得出.
解答 解:由等差数列的性质可得:a2+a16=a1+a17.
∵S17=34,
∴34=$\frac{17({a}_{1}+{a}_{17})}{2}$=$\frac{17({a}_{2}+{a}_{16})}{2}$,
∴a2+a16=4.
故选:C.
点评 本题考查了等差数列的性质、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在下面选项中,是x2-y2<0表示的平面区域是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列关系中,正确的是( )
| A. | sinα+cosβ=1 | B. | (sinα+cosα)2=1 | C. | sin2α+cos2α=1 | D. | sin2α+cos2β=1 |
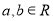 ,则“
,则“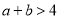 ”是“
”是“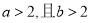 ”的( )
”的( )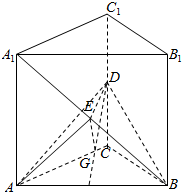 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.