题目内容
19.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点与抛物线y2=8x的焦点重合,且焦点到其渐近线的距离为1,则此双曲线的实轴长2$\sqrt{3}$.分析 由题意画出图形,再由抛物线方程求出焦点坐标,得到双曲线的焦点坐标,由焦点到双曲线一条渐近线的距离为1列式,再结合隐含条件求解.
解答 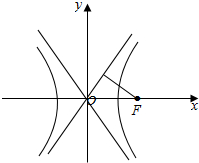 解:如图,
解:如图,
由抛物线方程y2=8x,得抛物线的焦点坐标F(2,0),
即双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点坐标为F(2,0),
双曲线的渐近线方程为$y=±\frac{b}{a}x$.
不妨取y=$\frac{b}{a}x$,化为一般式:bx-ay=0.
则$\frac{|2b|}{\sqrt{{a}^{2}+{b}^{2}}}=1$,即4b2=a2+b2,
又a2=4-b2,联立解得:a2=3,∴a=$\sqrt{3}$.
则双曲线的实轴长为$2\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查双曲线及抛物线的几何性质,考查了点到直线的距离公式的应用,是基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
14.已知an=$\left\{\begin{array}{l}{2n-1,n<2015}\\{(-\frac{1}{2})^{n-1},n≥2015}\end{array}\right.$,Sn是数列{an}的前n项和( )
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
11.在等差数列中,S17=34,则a2+a16等于( )
| A. | 17 | B. | 6 | C. | 4 | D. | 2 |
 为曲边的曲边形(如下图阴影部分)面积为 .
为曲边的曲边形(如下图阴影部分)面积为 .
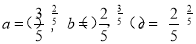 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( )