题目内容
下列函数中，值域是（0，+∞）的是（ ）A．y=x2+x，x∈[-1，+∞）
B．y=lnx，x∈[1，+∞）
C．y=|x|
D．y=
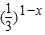
【答案】分析：利用配方法可求出函数y=x2+x的值域，利用y=lnx在[1，+∞）上的单调性可求出值域，根据绝对值函数的性质可求出y=|x|的值域，根据指数函数的性质可求出y=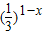
的值域，从而可判定正确选项．
解答：解：选项A，y=x2+x=（x+
）2-
，∵x∈[-1，+∞）∴y≥-
，故不正确；
选项B，y=lnx，在[1，+∞）上单调递增函数，故y≥0，故不正确；
选项C，y=|x|≥0，故不正确；
选项D，y=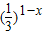
＞0，故正确
故选D．
点评：本题主要考查了二次函数、对数函数、指数函数等函数的值域，同时考查了计算能力，属于基础题．
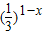的值域，从而可判定正确选项．解答：解：选项A，y=x2+x=（x+
）2-，∵x∈[-1，+∞）∴y≥-，故不正确；选项B，y=lnx，在[1，+∞）上单调递增函数，故y≥0，故不正确；
选项C，y=|x|≥0，故不正确；
选项D，y=
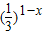＞0，故正确故选D．
点评：本题主要考查了二次函数、对数函数、指数函数等函数的值域，同时考查了计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
下列函数中，值域是[-2，2]的是（ ）
| A、f（x）=2x-1 | ||
| B、f（x）=log0.5（x+11） | ||
C、f（x）=
| ||
| D、f（x）=x2（4-x2） |
下列函数中，值域是（0，+∞）的函数是（ ）
A、y=x-
| ||
| B、y=x2+x+1 | ||
C、y=
| ||
| D、y=|log2（x+1）| |