题目内容
已知P为△ABC所在平面内一点,且满足
=
+
,则△APB的面积与△APC的面积之比为 .
| AP |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:
=
+
⇒
=3
-2
,继而可由
=
+
,
=
+
⇒
=2
,即P点是线段BC的靠近B点的三等分点,于是可得△PAC的面积与△ABC的面积之比.
| AP |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
| AC |
| AP |
| AB |
| BP |
| BA |
| AP |
| PC |
| PA |
| AC |
| PC |
| BP |
解答:
解:∵
=
+
,
=
+
,又∵
=
+
,
∴
=3
-2
,
∴
=
+
=
+(3
-2
)=2(
-
)=2
,即P点是线段BC的靠近B点的三等分点,
则△PAC的面积与△ABC的面积之比为:1:2,
故答案为:1:2.
| BP |
| BA |
| AP |
| PC |
| PA |
| AC |
| AP |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
∴
| AC |
| AP |
| AB |
∴
| PC |
| PA |
| AC |
| PA |
| AP |
| AB |
| AP |
| AB |
| BP |
则△PAC的面积与△ABC的面积之比为:1:2,
故答案为:1:2.
点评:本题考查平面向量的基本定理及其意义,求得
=2
是关键,也是难点,考查转化思想与运算求解能力.
| PC |
| BP |

练习册系列答案
相关题目
定义运算
=
,称
=
为将点(x,y)映到点(x′,y′)的一次变换.若
=
把直线y=x上的各点映到这点本身,而把直线y=3x上的各点映到这点关于原点对称的点.则p,q的值分别是( )
|
|
|
|
|
|
|
|
| A、p=1,q=1 |
| B、p=3,q=1 |
| C、p=3,q=3 |
| D、p=3,q=-2 |
 如图,在四棱锥P-ABCD中,底面四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,则二面角P-CD-B的大小是
如图,在四棱锥P-ABCD中,底面四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,则二面角P-CD-B的大小是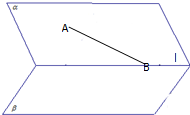 如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )
如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )