题目内容
13．已知△ABC的三边长a，b，c成递减的等差数列，若$B=\frac{π}{4}$，则cosA-cosC=（ ）| A． | $-\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $-\root{4}{2}$ | D． | $\root{4}{2}$ |
分析 三边a，b，c成等差数列，可得2b=a+c，利用正弦定理可得：2sinB=sinA+sinC，即sinA+sinC=$\sqrt{2}$，设cosA-cosC=m，平方相加即可得出．
解答 解：∵三边a，b，c成等差数列，
∴2b=a+c，
利用正弦定理可得：2sinB=sinA+sinC，
∴sinA+sinC=2sin$\frac{π}{4}$=$\sqrt{2}$，
设cosA-cosC=m，
则平方相加可得：2-2cos（A+C）=2+m2，
∴m2=2cosB=$\sqrt{2}$，
解得m=±$\root{4}{2}$．
∵a，b，c成递减的等差数列，
∴m=-$\root{4}{2}$．
故选：C．
点评 本题考查了等差数列的通项公式性质、正弦定理、同角三角函数基本关系式、和差公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
3．若函数f（2x+1）的定义域为（-1，0），则函数f（x）的定义域为（ ）
| A． | （-2，0） | B． | （-1，0） | C． | （-1，1） | D． | （0，1） |
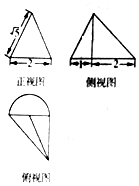某几何体上的三视图如图所示，则该几何体的体积是$\frac{4+π}{3}$．