题目内容
6.过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线的双曲线方程是( )| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
分析 由已知可设双曲线的方程为:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),由于过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线,可得$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}-\frac{4}{{b}^{2}}=1}\\{\frac{a}{b}=\frac{\sqrt{2}}{2}}\end{array}\right.$,解出即可得出.
解答 解:由已知可设双曲线的方程为:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),
∵过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线,
∴$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}-\frac{4}{{b}^{2}}=1}\\{\frac{a}{b}=\frac{\sqrt{2}}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\sqrt{2}}\\{b=2}\end{array}\right.$,
∴双曲线的方程为:$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{4}$=1.
故选:A.
点评 本题考查了双曲线的标准方程及其性质、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.设集合A={x|x2-x-2<0},B={x|-1<x<1},则( )
| A. | A?B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
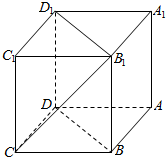 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,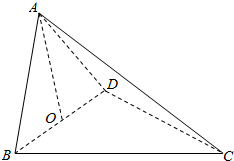 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.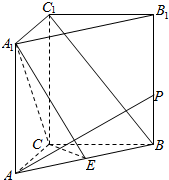 如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.
如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.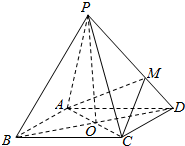 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.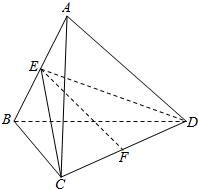 如图,正四面体ABCD的棱长为1.
如图,正四面体ABCD的棱长为1.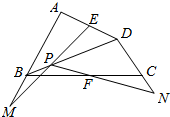 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.


