题目内容
2.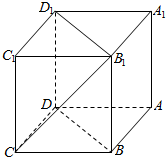 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是AB、AD、AA1的中点,(1)求证:平面CB1D1∥平面MNP;
(2)求平面CB1D1与平面MNP的距离.
分析 (1)连结A1B、A1D,根据正方体的性质证出四边形A1D1CB是平行四边形,可得A1B∥D1C,由三角形中位线定理得PM∥A1B,从而得到PM∥D1C,利用线面平行判定定理证出PM∥平面CB1D1,同理可得MN∥平面CB1D1.最后利用面面平行判定定理即可证出平面MNP∥平面CB1D1.
(2)由题意,AC1被平面CB1D1、平面A1BD截成相等的3部分,距离为$\frac{\sqrt{3}}{3}$a,A到平面MNP的距离为$\frac{\sqrt{3}}{6}$a,即可求出平面CB1D1与平面MNP的距离.
解答 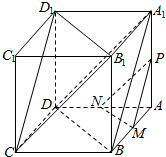 (1)证明:连结A1B、A1D,
(1)证明:连结A1B、A1D,
∵正方体ABCD-A1B1C1D1中,A1D1平行且等于BC,
∴四边形A1D1CB是平行四边形,可得A1B∥D1C,
∵PM是△AA1B的中位线,可得PM∥A1B,∴PM∥D1C,
∵PM?平面CB1D1,D1C?平面CB1D1,
∴PM∥平面CB1D1,
同理可得:MN∥平面CB1D1,
∵PM、MN是平面MNP内的相交直线,
∴平面MNP∥平面CB1D1.
(2)解:由题意,AC1被平面CB1D1、平面A1BD截成相等的3部分,距离为$\frac{\sqrt{3}}{3}$a,A到平面MNP的距离为$\frac{\sqrt{3}}{6}$a,
∴平面CB1D1与平面MNP的距离为$\frac{\sqrt{3}}{3}$a+$\frac{\sqrt{3}}{6}$a=$\frac{\sqrt{3}}{2}$a.
点评 本题证明正方体中的面面平行,考查了正方体的性质、线面平行与面面平行的判定定理,考查平面与平面间的距离等知识,属于中档题.

练习册系列答案
相关题目
7.已知二面角α-l-β为60°,如果平面角α内一点A到平面β的距离为$\sqrt{3}$,那么A到棱的距离为( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
6.过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线的双曲线方程是( )
| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
 B.
B.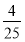 C.
C.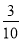 D.
D.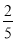
 ,则cos(α+
,则cos(α+ )=( )
)=( ) B.
B. C.
C. D.
D.
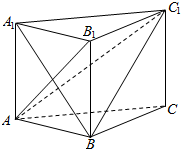 如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.
如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.