Question

16．函数f（x）=$\frac{{{x^2}sinx}}{{{{1.5}^{|x|}}}}$的图象大致为（　　）

• A．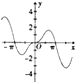
• B．
• C．
• D．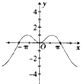

Answer 1

分析 分析四个图象的不同，从而判断函数的性质，利用排除法求解．

解答 解：∵f（-x）=$\frac{（-x）^{2}sin（-x）}{1．{5}^{|x|}}$=-f（x），
∴f（x）是奇函数，
∴f（x）的图象关于原点对称，
故排除D；
易知f（$\frac{π}{4}$）＞0，故排除B；
f（π）=0，故排除C；
故选A．

点评 本题考查了函数的性质的判断与数形结合的思想方法应用．