题目内容
1．等比数列{an}的公比$\frac{1}{2}$，前n项和为Sn，则$\frac{{S}_{4}}{{a}_{4}}$=（ ）| A． | 31 | B． | 15 | C． | 7 | D． | 1 |
分析 设等比数列{an}的首项为a1，利用公比为$\frac{1}{2}$，将分子、分母都用首项a1表示，即可得到结论．
解答 解：由题意，设等比数列{an}的首项为a1，
∵公比为q=$\frac{1}{2}$，
∴$\frac{{S}_{4}}{{a}_{4}}$=$\frac{\frac{{a}_{1}（1-\frac{1}{16}）}{1-\frac{1}{2}}}{{a}_{1}×\frac{1}{8}}$=15．
故选：B．
点评 本题考查等比数列，考查等比数列的通项与求和，正确运用公式是关键．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
9．若集合A={1，2，3，4，5}，集合B={x|x（4-x）＜0}，则图中阴影部分表示（ ）
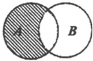
| A． | {1，2，3，4} | B． | {1，2，3} | C． | {4，5} | D． | {1，4} |
6．已知集合E={x∈R|x2-2x＞0}，F={x∈R|log2（x+1）＜2}，则（ ）
| A． | E∩F=∅ | B． | E∪F=R | C． | E⊆F | D． | F⊆E |
13．下面各组函数中为相等函数的是（ ）
| A． | f（x）=$\sqrt{{{（x-1）}^2}}$，g（x）=x-1 | B． | f（x）=x-1，g（t）=t-1 | ||
| C． | f（x）=$\sqrt{{x^2}-1}$，g（x）=$\sqrt{x+1}$•$\sqrt{x-1}$ | D． | f（x）=x，g（x）=$\frac{x^2}{x}$ |