题目内容
11．已知在△ABC中，AB=3，AC=7，点P在AC上，且PB=PC，则$\overrightarrow{AP}$•$\overrightarrow{BC}$=20．分析 以A为原点，以AC为x轴建立坐标系，设∠BAC=θ，AP=x，求出$\overrightarrow{AP}，\overrightarrow{BC}$的坐标，根据PB=PC列方程得出cosθ与x的关系，代入向量的数量积公式计算即可．
解答 解：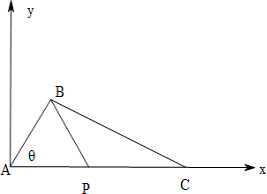
以A为原点，以AC为x轴建立平面直角坐标系，设∠BAC=θ，AP=x，
则A（0，0），B（3cosθ，3sinθ），P（x，0），C（7，0）．
∴$\overrightarrow{AP}$=（x，0），$\overrightarrow{BC}$=（7-3cosθ，-3sinθ），
∵PB=PC，
∴$\sqrt{（x-3cosθ）^{2}+（3sinθ）^{2}}$=7-x，
即x2-6xcosθ+9=49-14x+x2，
∴cosθ=$\frac{7x-20}{3x}$．
∴$\overrightarrow{AP}•\overrightarrow{BC}$=（7-3cosθ）x=7x-3xcosθ=20．
故答案为：20．
点评 本题考查了平面向量的数量积运算，坐标法是常用方法之一．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
3．在△ABC中，$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$，$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则$\overrightarrow{PQ}$=（ ）
| A． | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D． | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ |
