题目内容
4.已知函数f(x)的定义域为(0,+∞),对于定义域内任意x,y,均有f(xy)=f(x)+f(y),且函数在定义域内为单调递减函数.(Ⅰ)求$f(1),f(a)+f({\frac{1}{a}})$的值;
(Ⅱ)求函数f(x)的零点;
(Ⅲ)求满足不等式f(2m+1)+f(m)>0的实数m的范围.
分析 (Ⅰ)特殊值法:令x=y=1得f(1)=f(1)+f(1),解得f(1)=0,令x=a,y=$\frac{1}{a}$,求解即可;
(Ⅱ)函数在定义域内为单调递减函数,可判断函数有唯一零点,即x=1;
(Ⅲ)根据条件f(2m+1)+f(m)>0,可得f(2m+1)+f(m)>f(1),根据函数的性质和单调性可得(m+1)(2m-1)<0,求解即可.
解答 解:(Ⅰ)由题意知,f(xy)=f(x)+f(y)
令x=y=1得f(1)=f(1)+f(1),解得f(1)=0,
令x=a,y=$\frac{1}{a}$,
∴f(a)+f($\frac{1}{a}$)=f(1)=0;
(Ⅱ)∵函数在定义域内为单调递减函数,
∵f(1)=0,
∴在定义域内只有一个零点x=1;
(Ⅲ)f(2m+1)+f(m)>0,
∴f(2m+1)+f(m)>f(1),
∴(m+1)(2m-1)<0,
∴-1<m<$\frac{1}{2}$,
∵m>0,
∴0<m<$\frac{1}{2}$
点评 考查了抽象函数的特殊值法应用和利用函数的性质解决实际问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
9.若集合A={1,2,3,4,5},集合B={x|x(4-x)<0},则图中阴影部分表示( )
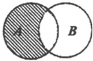

| A. | {1,2,3,4} | B. | {1,2,3} | C. | {4,5} | D. | {1,4} |
13.下面各组函数中为相等函数的是( )
| A. | f(x)=$\sqrt{{{(x-1)}^2}}$,g(x)=x-1 | B. | f(x)=x-1,g(t)=t-1 | ||
| C. | f(x)=$\sqrt{{x^2}-1}$,g(x)=$\sqrt{x+1}$•$\sqrt{x-1}$ | D. | f(x)=x,g(x)=$\frac{x^2}{x}$ |