题目内容
1．在△ABC中，$a=2，b=4，C={30°}，则\overrightarrow{BC}•\overrightarrow{CA}$=（ ）| A． | $4\sqrt{3}$ | B． | 4 | C． | -4$\sqrt{3}$ | D． | -4 |
分析 直接利用向量的数量积的公式求解即可．
解答 解：在△ABC中，$a=2，b=4，C={30°}，则\overrightarrow{BC}•\overrightarrow{CA}$=a•bcos30°=2×$4×\frac{\sqrt{3}}{2}$=4$\sqrt{3}$．
故选：A．
点评 本题考查向量的数量积的求法，考查计算能力．
练习册系列答案
相关题目
12．一个几何体的三视图如图所示，则该几何体的体积为（ ）
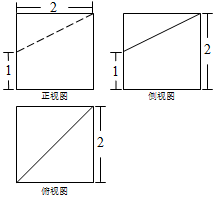
| A． | $\frac{22}{3}$ | B． | $\frac{20}{3}$ | C． | $\frac{16}{3}$ | D． | 6 |
16．观察数表（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），（43），…，则第100个括号内各数之和为（ ）
| A． | 1479 | B． | 1992 | C． | 2000 | D． | 2072 |
6．已知函数f（x）=（x3+2x2+ax-a）ex，f′（x）为f（x）的导函数，则f′（0）的值为（ ）
| A． | 0 | B． | 1 | C． | -a | D． | 不确定 |
10．某小学为了解本校某年级女生的身高情况，从本校该年级的学生中随机选出100名女生并统计她们的身高（单位：cm），得到如图频率分布表：
（Ⅰ）用分层抽样的方法从身高在[125，130）和[140，145]的女生中共抽取6人，则身高在[125，130）的女生应抽取几人？
（Ⅱ）在（Ⅰ）中抽取的6人中，再随机抽取2人，求这2人身高都在[125，130）内的概率．
| 分组（身高） | [125，130） | [130，135） | [135，140） | [140，145] |
（Ⅱ）在（Ⅰ）中抽取的6人中，再随机抽取2人，求这2人身高都在[125，130）内的概率．