题目内容
7.不等式$|\begin{array}{l}{x}&{1}\\{3}&{x}\end{array}|$+2x>0的解集为{x|x<-3或x>1}.分析 由二阶行列式的展开法则,把原不等式等价转化为x2+2x-3>0,由此能求出不等式$|\begin{array}{l}{x}&{1}\\{3}&{x}\end{array}|$+2x>0的解集.
解答 解:∵$|\begin{array}{l}{x}&{1}\\{3}&{x}\end{array}|$+2x>0,
∴x2+2x-3>0,
解得x<-3或x>1,
∴不等式$|\begin{array}{l}{x}&{1}\\{3}&{x}\end{array}|$+2x>0的解集为{x|x<-3或x>1}.
故答案为:{x|x<-3或x>1}.
点评 本题考查不等式的解法,是基础题,解题时要认真审题,注意二阶行列式展开法则的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知球面上有A、B、C三点,BC=2$\sqrt{3}$,AB=AC=2,若球的表面积为20π,则球心到平面ABC的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
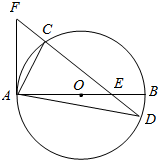 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
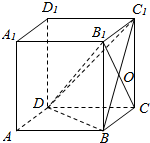 如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.
如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.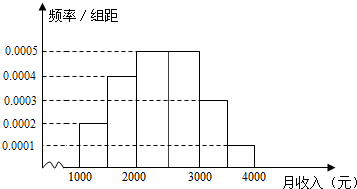 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )