题目内容
17.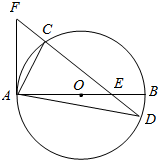 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.(1)证明:AF•DA=AC•DF
(2)若圆的半径为2,OE=EB=$\frac{1}{2}$AF,ED=$\frac{3}{2}$,求CF的长.
分析 (1)证明△CAF∽△ADF,即可证明AF•DA=AC•DF
(2)CE•ED=AE•EB,可得CE=2,AF2=FC•FD,即4=FC•(FC+2+1),即可求CF的长.
解答 (1)证明:∵AB是圆O的直径,AF⊥AB,
∴∠CAF=∠ADF,
∴△CAF∽△ADF,
∴$\frac{CA}{AD}=\frac{AF}{DF}$,
∴AF•DA=AC•DF
(2)解:∵圆的半径为2,OE=EB,ED=$\frac{3}{2}$,
∴CE•ED=AE•EB,即CE•$\frac{3}{2}$=3•1,∴CE=2
∵AF=2,AF是切线,
∴AF2=FC•FD,即4=FC•(FC+2+1),
∴FC=1.
点评 本题考查三角形相似的判定与性质,考查相交弦定理,切割线定理,考查相似分析解决问题的能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
8.一个球的表面积为36π,则这个球体的体积为( )
| A. | 18π | B. | 36π | C. | 72π | D. | 108π |
6.已知正实数a、b、c满足$\frac{1}{e}≤\frac{c}{a}$≤2,clnb=a+clnc,其中e是自然对数的底数,则ln$\frac{b}{a}$的取值范围是( )
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
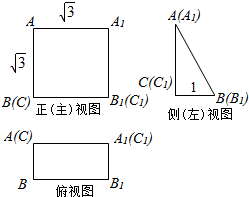 一个空间几何体的三视图及部分数据如图所示.
一个空间几何体的三视图及部分数据如图所示.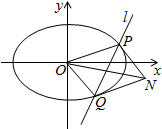 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.