题目内容
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为
(α为参数).
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
),判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值.
(Ⅲ)请问是否存在直线m,m∥l且m与曲线C的交点A、B满足S△ABC=
;若存在请求出满足题意的所有直线方程,若不存在请说明理由.
|
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
| π |
| 2 |
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值.
(Ⅲ)请问是否存在直线m,m∥l且m与曲线C的交点A、B满足S△ABC=
| 3 |
| 4 |
考点:简单曲线的极坐标方程,椭圆的参数方程
专题:圆锥曲线的定义、性质与方程
分析:(I)利用极坐标与直角坐标的互化公式即可得出;
(II)设Q(
cos,sinα),利用点到直线的距离公式可得点Q到直线l的距离d,再利用余弦函数的单调性即可得出;
(III)假设存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
.
设A(x1,y1),B(x2,y2).设直线l:x-y+t=0.由曲线C的参数方程为
(α为参数),化为
+y2=1.联立方程得到△>0及根与系数的关系,利用弦长公式可得|AB|,利用点到直线的距离公式可得原点O到直线m的距离,再利用三角形的面积计算公式即可得出.
(II)设Q(
| 3 |
(III)假设存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
| 3 |
| 4 |
设A(x1,y1),B(x2,y2).设直线l:x-y+t=0.由曲线C的参数方程为
|
| x2 |
| 3 |
解答:
解:(I)由P(4,
)可得xP=4cos
=0,yP=4sin
=4.∴P(0,4).
把P(0,4)代入直线l的方程:0-4+4=0,满足直线l的方程,因此点P在直线l上.
(II)设Q(
cos,sinα),∴点Q到直线l的距离d=
=
.
∵-1≤cos(α+
)≤1,∴2≤2cos(α+
)+4≤6.
∴
≤d≤
,即
≤d≤3
.
点Q到直线l的距离的最大值是3
,最小值是
.
(III)假设存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
.
设A(x1,y1),B(x2,y2).
设直线l:x-y+t=0.由曲线C的参数方程为
(α为参数),化为
+y2=1.
联立
,化为4x2+6tx+3t2-3=0.
∵直线l与椭圆有两个交点,∴△=36t2-16(3t2-3)>0,化为t2<4(*).
∴x1+x2=-
,x1x2=
.
∴|AB|=
=
,
原点O到直线l的距离d=
,
∴
|AB|d=
,
∴
×
=
,化为t4-4t2+3=0,解得t2=1或t2=3.满足(*).
∴存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
,
直线l为x-y±1=0,或x-y±
=0.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
把P(0,4)代入直线l的方程:0-4+4=0,满足直线l的方程,因此点P在直线l上.
(II)设Q(
| 3 |
|
| ||
|
|2cos(α+
| ||
|
∵-1≤cos(α+
| π |
| 6 |
| π |
| 6 |
∴
| 2 | ||
|
| 6 | ||
|
| 2 |
| 2 |
点Q到直线l的距离的最大值是3
| 2 |
| 2 |
(III)假设存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
| 3 |
| 4 |
设A(x1,y1),B(x2,y2).
设直线l:x-y+t=0.由曲线C的参数方程为
|
| x2 |
| 3 |
联立
|
∵直线l与椭圆有两个交点,∴△=36t2-16(3t2-3)>0,化为t2<4(*).
∴x1+x2=-
| 3t |
| 2 |
| 3t2-3 |
| 4 |
∴|AB|=
(1+1)[(
|
|
原点O到直线l的距离d=
| |t| | ||
|
∴
| 1 |
| 2 |
| 3 |
| 4 |
∴
| 1 |
| 2 |
|
| |t| | ||
|
| 3 |
| 4 |
∴存在直线m,m∥l且m与曲线C的交点A、B满足S△AOB=
| 3 |
| 4 |
直线l为x-y±1=0,或x-y±
| 3 |
点评:本题综合考查了极坐标与直角坐标的互化公式、点到直线的距离公式、余弦函数的单调性、相互平行的直线的斜率之间的关系、椭圆的参数方程、直线与椭圆相交问题转化为方程联立得到△>0及根与系数的关系、弦长公式、三角形的面积计算公式等基础知识与基本技能方法,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式-x2-5x+6≥0的解集为( )
| A、{x|x≤-6或x≥1} |
| B、{x|x≥6或x≤-1} |
| C、{x|-6≤x≤1} |
| D、{x|-1≤x≤6} |
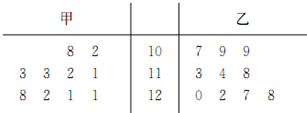 为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)
为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)