题目内容
8．计算-sin133°cos197°-cos47°cos73°的结果为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 由条件利用诱导公式、两角和差的正弦公式，化简所给的式子，可得结果．
解答 解：-sin133°cos197°-cos47°cos73°=-sin47°（-cos17°）-cos47°sin17°
=sin（47°-17°）=sin30°=$\frac{1}{2}$，
故选：A．
点评 本题主要考查诱导公式、两角和差的正弦公式的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．
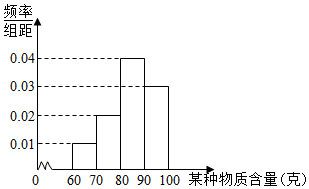某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如图所示．
（I）估计产品中该物质含量的平均数及方差（同一组数据用该区间的中点值作代表）；
（Ⅱ）规定产品的级别如表：
现质检部门从三个等级的产品中采用分层抽样的方式抽取10件产品，再从中随机抽取3件产品进行检测，记质检部门“抽到B或C级品的个数为ξ”，求ξ的分布列和数学期望．
某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如图所示．（I）估计产品中该物质含量的平均数及方差（同一组数据用该区间的中点值作代表）；
（Ⅱ）规定产品的级别如表：
| 产品级别 | C | B | A |
| 某押麴质含量范围 | [60，70） | [70，80） | [80，100] |
20．已知不等式2x+m+$\frac{8}{x-1}$＞0对一切x∈（1，+∞）恒成立，则实数m的取值范围是（ ）
| A． | m＞-10 | B． | m＜-10 | C． | m＞-8 | D． | m＜-8 |