题目内容
17.在三角形ABC中,角A,B,C的对边分别是a,b,c.若b=$\sqrt{2}$,c=3,B+C=3A.(1)求边a;
(2)求sin(B+$\frac{3π}{4}$)的值.
分析 (1)由条件利用余弦定理求得a的值.
(2)由条件利用正弦定理求得sinB的值,可得cosB的值,再利用两角和差的正弦公式,求得sin(B+$\frac{3π}{4}$)的值.
解答 解:(1)三角形ABC中,∵b=$\sqrt{2}$,c=3,B+C=3A,
∴A=$\frac{π}{4}$,利用余弦定理可得a2=b2+c2-2bc•cosA=5,∴a=$\sqrt{5}$.
(2)由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$,可得$\frac{\sqrt{5}}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{sinB}$,∴sinB=$\frac{\sqrt{5}}{5}$,
再结合b<c,可得B为锐角,∴cosB=$\sqrt{{1-sin}^{2}B}$=$\frac{2\sqrt{5}}{5}$,
∴sin(B+$\frac{3π}{4}$)=sinBcos$\frac{3π}{4}$+cosBsin$\frac{3π}{4}$=$\frac{\sqrt{5}}{5}•(-\frac{\sqrt{2}}{2})$+$\frac{2\sqrt{5}}{5}$•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{10}}{10}$.
点评 本题主要考查两角和差的正弦公式的应用,正弦定理和余弦定理,属于基础题.

练习册系列答案
相关题目
7.复数z=i(3+2i)(其中i为虚数单位)所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.计算-sin133°cos197°-cos47°cos73°的结果为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(1-x)(x<0)}\\{g(x)+1(x>0)}\end{array}\right.$,若f(x)是奇函数,则g(3)的值是( )
| A. | 1 | B. | 3 | C. | -3 | D. | -1 |
6.欧拉公式eiθ=cosθ+isinθ(e为自然对数的底数,i为虚数单位)是瑞士著名数学家欧拉发明的,eiπ+1=0被英国科学期刊《物理世界》评选为十大最伟大的公式之一,根据欧拉公式可知,复数${e^{-\frac{π}{6}i}}$的虚部为( )
| A. | $-\frac{1}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
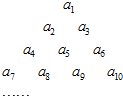 设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….
设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….