题目内容
已知α是三角形的最大内角,且cos2α=
,则曲线
+
=1的离心率为( )
| 1 |
| 2 |
| x2 |
| cosα |
| y2 |
| sinα |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质,二倍角的余弦
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出α=150°,曲线
+
=1等价转化为
-
=1,由此能求出结果.
| x2 |
| cosα |
| y2 |
| sinα |
| y2 | ||
|
| x2 | ||||
|
解答:
解:∵α是三角形的最大内角,且cos2α=
,
∴2α=300°,∴α=150°,
∴cosα=cos150°=-cos30°=-
,
sinα=sin150°=sin30°=
,
∵曲线
+
=1,
∴
-
=1,
∴a=
,c=
,
∴e=
=
=
.
故选:D.
| 1 |
| 2 |
∴2α=300°,∴α=150°,
∴cosα=cos150°=-cos30°=-
| ||
| 2 |
sinα=sin150°=sin30°=
| 1 |
| 2 |
∵曲线
| x2 |
| cosα |
| y2 |
| sinα |
∴
| y2 | ||
|
| x2 | ||||
|
∴a=
|
|
∴e=
| c |
| a |
| ||||||
|
1+
|
故选:D.
点评:本题考查双曲线的求法,是中档题,解题时要熟练掌握三角函数的性质.

练习册系列答案
相关题目
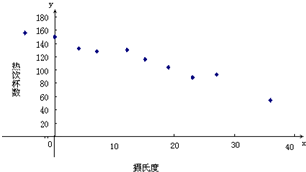 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程 |
| y |
| A、气温与热饮的销售杯数之间成正相关 | ||
| B、当天气温为2°C时,这天大约可以卖出143杯热饮 | ||
| C、当天气温为10°C时,这天恰卖出124杯热饮 | ||
D、由于x=0时,
|
 一几何体的三视图如图所示,则该几何体的体积为( )
一几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、
| ||
C、(16+4
| ||
D、
|
设m,n为不同的直线,α,β为不同的平面,有如下四个命题:
①若m∥α,n?α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α⊥β,m⊥α,则m∥β;
④若m⊥α,n∥β且α∥β,则m⊥n.
其中错误命题的个数是( )
①若m∥α,n?α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α⊥β,m⊥α,则m∥β;
④若m⊥α,n∥β且α∥β,则m⊥n.
其中错误命题的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
若变量x,y满足约束条件
,则目标函数z=3x-y的最小值为( )
|
| A、-4 | ||
| B、0 | ||
C、
| ||
| D、4 |
一个几何体的三视图如图所示,则该几何体的体积是( )


| A、8 | B、10 | C、12 | D、14 |
 已知椭圆C的方程为
已知椭圆C的方程为