题目内容
设m,n为不同的直线,α,β为不同的平面,有如下四个命题:
①若m∥α,n?α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α⊥β,m⊥α,则m∥β;
④若m⊥α,n∥β且α∥β,则m⊥n.
其中错误命题的个数是( )
①若m∥α,n?α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α⊥β,m⊥α,则m∥β;
④若m⊥α,n∥β且α∥β,则m⊥n.
其中错误命题的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①利用线面平行的性质定理即可判断出;
②利用线面面面平行的性质定理与判定定理即可判断出;
③利用面面垂直的性质定理即可判断出;
④利用线面的平行与垂直判定与性质定理即可判断出.
②利用线面面面平行的性质定理与判定定理即可判断出;
③利用面面垂直的性质定理即可判断出;
④利用线面的平行与垂直判定与性质定理即可判断出.
解答:
解:①若m∥α,n?α,利用线面平行的性质定理可知:m∥n或为异面直线,因此不正确;
②若m∥α,m∥β,则α∥β或相交,因此不正确;
③若α⊥β,m⊥α,利用面面垂直的性质定理即可判断出m∥β或m?β,因此不正确;
④若m⊥α,n∥β且α∥β,利用线面的位置关系可得:m⊥n,正确.
综上可知:只有①②③错误.
故选:D.
②若m∥α,m∥β,则α∥β或相交,因此不正确;
③若α⊥β,m⊥α,利用面面垂直的性质定理即可判断出m∥β或m?β,因此不正确;
④若m⊥α,n∥β且α∥β,利用线面的位置关系可得:m⊥n,正确.
综上可知:只有①②③错误.
故选:D.
点评:本题综合考查了空间中线面面面的位置关系及其判定方法,属于基础题.

练习册系列答案
相关题目
已知α是三角形的最大内角,且cos2α=
,则曲线
+
=1的离心率为( )
| 1 |
| 2 |
| x2 |
| cosα |
| y2 |
| sinα |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设平面α、β,直线a、b,a?α,b?α,则“a∥β,b∥β”是“α∥β”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列四个结论:
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
(1)两条直线都和同一个平面平行,则这两条直线平行;
(2)两条直线没有公共点,则这两条直线平行;
(3)两条直线都和第三条直线垂直,则这两条直线平行;
其中正确的命题个数为( )
| A、0 | ||
| B、1 | ||
| C、π | ||
D、
|
执行如图所示的程序框图,则输出S的值为( )
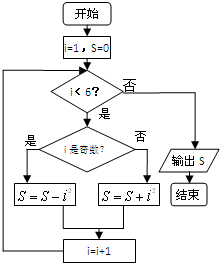

| A、3 | B、-6 | C、10 | D、-15 |
 正四面体ABCD边长为2.E,F分别为AC,BD中点.
正四面体ABCD边长为2.E,F分别为AC,BD中点.