题目内容
18.已知函数f(x)=$\sqrt{3}$sinxcosx-cos2x,x∈R.(1)将函数化为f(x)=Asin(ωx+ϕ)+b形式.
(2)求函数的最大值,并求此时x的相应值.
分析 (1)利用三角恒等变换化简函数的解析式,可得结论.
(2)利用正弦函数的定义域和值域求得函数f(x)的最大值,以及此时x的相应值.
解答 解:(1)函数f(x)=$\sqrt{3}$sinxcosx-cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1+cos2x}{2}$=sin(2x-$\frac{π}{6}$)-$\frac{1}{2}$.
(2)∵当2x-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z时,sin(2x-$\frac{π}{6}$)取得最大值为1,
故f(x)的最大值为1-$\frac{1}{2}$=$\frac{1}{2}$,此时,x=kπ+$\frac{π}{3}$,k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如果数据x1,x2,…,xn的平均数为2,方差为3,则数据3x1+5,3x2+5…,3xn+5的平均数和方差分别为( )
| A. | 11,25 | B. | 11,27 | C. | 8,27 | D. | 11,8 |
13.已知点M(-1,6),N(3,2),则线段MN的垂直平分线方程为( )
| A. | x-y-4=0 | B. | x-y+3=0 | C. | x+y-5=0 | D. | x+4y-17=0 |
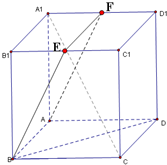 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点. 2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,
2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,