题目内容
一只蚂蚁在高为3,两底分别为3和6的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为 .
考点:几何概型
专题:概率与统计
分析:以四个顶点为圆心,1为半径作圆,当蚂蚁在此区域外的区域随机爬行,离顶点的距离大于1,其面积为
-π,再用几何概型公式即得本题的概率.
| 27 |
| 2 |
解答:
解:如图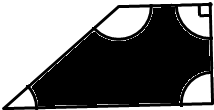 由已知,高为3,两底分别为3和6的直角梯形面积为
由已知,高为3,两底分别为3和6的直角梯形面积为
×3×(3+6)=
,
离四个顶点距离都大于1的区域是如图阴影部分,即以四个顶点为圆心,1为半径作圆,当蚂蚁在除此区域外的区域随机爬行,离顶点的距离大于1的部分,其面积为
×3×(3+6)-π=
-π,
∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=
=1-
.
故答案为:1-
.
 由已知,高为3,两底分别为3和6的直角梯形面积为
由已知,高为3,两底分别为3和6的直角梯形面积为| 1 |
| 2 |
| 27 |
| 2 |
离四个顶点距离都大于1的区域是如图阴影部分,即以四个顶点为圆心,1为半径作圆,当蚂蚁在除此区域外的区域随机爬行,离顶点的距离大于1的部分,其面积为
| 1 |
| 2 |
| 27 |
| 2 |
∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=
| ||
|
| 2π |
| 27 |
故答案为:1-
| 2π |
| 27 |
点评:本题以蚂蚁在正方形内爬行为例,求几何概型的概率.着重考查了图形面积的求法和几何概型的概率求法等知识点,属于基础题.

练习册系列答案
相关题目
设不等式组
表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知椭圆和双曲线右公共焦点F1、F2,P是它们的一个公共点,且∠F1PF2=
,若双曲线的离心率为
,则椭圆的离心率为( )
| π |
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
4张奖券中只有1张能中奖,现分别由4名同学无放回地抽取.若已知第一名同学没有抽到中奖券,则第二名同学抽到中奖券的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |