题目内容
7.已知幂函数y=f(x)的图象经过点(3,9),对于偶函数y=g(x)(x∈R),当x≥0时.g(x)=f(x)-2x.(1)求函数y=f(x)的解析式;
(2)求当x<0时,函数y=g(x)的解析式,并在给定坐标系下,画出函数y=g(x)的图象;
(3)写出函数y=|g(x)|的单调递减区间.
分析 (1)∵幂函数y=xα,代入点的坐标可得3α=9,解方程可得;
(2)当x<0时,-x>0,由题意可得g(-x)=x2+2x,再由偶函数可得解析式,可作出图象;
(3)由对称性结合(2)的图象可得函数y=|g(x)|的图象,数形结合可得单调区间.
解答 解:(1)∵幂函数y=f(x)=xα的图象经过点(3,9),
∴3α=9,解得α=2,
∴函数y=f(x)的解析式为f(x)=x2;
(2)∵偶函数y=g(x)(x∈R),
当x≥0时,g(x)=x2-2x,
∴当x<0时,-x>0,则g(-x)=x2+2x,
由函数为偶函数可得当x<0时,
g(x)=g(-x)=x2+2x,
函数y=g(x)的图象如图所示;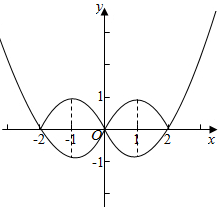
(3)只需将(2)的图象x轴上方的不动,x轴下方的作关于x轴的对称,
可得函数y=|g(x)|的图象(图中红色为对称后的图象),
结合图象可得函数y=|g(x)|的单调递减区间为(-∞,-2)和(-1,0)和(1,2)
点评 本题考查函数的解析式求解的常用方法,涉及函数奇偶性和图象的对称性,属中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
18.将函数f(x)=sin2x的图象向左平移$\frac{π}{6}$个单位后与函数g(x)的图象重合,则函数g(x)为( )
| A. | $sin(2x-\frac{π}{6})$ | B. | $sin(2x+\frac{π}{6})$ | C. | $sin(2x-\frac{π}{3})$ | D. | $sin(2x+\frac{π}{3})$ |
15.在各项均为正数的等比数列{an}中,a5a6=4,则数列{log2an}的前10项和等于( )
| A. | 20 | B. | 10 | C. | 5 | D. | 2+log25 |
2.定义A°B={x|x∈A或x∈B,但x∉A∩B}.已知M={y|y=2|x|},N={x|$\frac{3}{2-x}$≤2},则M°N=( )
| A. | [0,1)∪(2,+∞) | B. | (-∞,$\frac{1}{2}$]∪[1,2] | C. | [$\frac{1}{2}$,1)∪(2,+∞) | D. | [1,2) |
12.设i为虚数单位,已知复数z满足$\frac{z}{z-2i}$=i,则其共轭复数$\overline z$为( )
| A. | 1+i | B. | $\sqrt{2}$+$\sqrt{2}$i | C. | 1-i | D. | $\sqrt{2}$-$\sqrt{2}$i |