题目内容
阅读下表后,请应用类比的思想,得出椭圆中的结论:
| 圆 | 椭圆 | |
| 定 义 |
平面上到动点P到定点O的距离等于定长的点的轨迹 | 平面上的动点P到两定点F1,F2的距离之和等于定值2a的点的轨迹(2a>|F1F2|) |
| 结 论 |
如图,AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆O上任意一点, CD是过P的切线,则有“PO2=PC•PD” 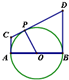 |
椭圆的长轴为AB,O是椭圆的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A,B的切线,P是椭圆上任意一点,CD是过P的切线,则有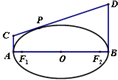 |
考点:类比推理
专题:简易逻辑,推理和证明
分析:类比圆的半径和椭圆的焦半径,不难发现关系:OP2和PF1•PF2具有等价性.
解答:
解:由题意可知:圆的半径和椭圆的焦半径,是类比对象,
不难发现关系:OP2和PF1•PF2具有等价性.
在圆中有PO2=PC•PD.则椭圆中PF1•PF2=PC•PD
故答案为:PF1•PF2=PC•PD
不难发现关系:OP2和PF1•PF2具有等价性.
在圆中有PO2=PC•PD.则椭圆中PF1•PF2=PC•PD
故答案为:PF1•PF2=PC•PD
点评:本题主要考查了类比推理,关键是需要找到类比对象,本题是中档题.

练习册系列答案
相关题目
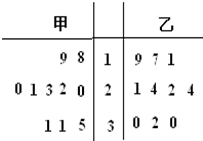 甲、乙两人在10天中每天加工的零件的个数用茎叶图表示如图.中间一列的数字表示零件个数的十位数,两边的数字零件个数的个位数,则这10天中甲、乙两人日加工零件的平均水平
甲、乙两人在10天中每天加工的零件的个数用茎叶图表示如图.中间一列的数字表示零件个数的十位数,两边的数字零件个数的个位数,则这10天中甲、乙两人日加工零件的平均水平