题目内容
16.若向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{b}$|=4,($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-3$\overrightarrow{b}$)=-72,则向量$\overrightarrow{a}$的模为( )| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
分析 根据平面向量数量积与夹角、模长的关系计算($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-3$\overrightarrow{b}$)=-72,即可求出$\overrightarrow{a}$的模长.
解答 解:向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{b}$|=4,
且($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-3$\overrightarrow{b}$)=|$\overrightarrow{a}$|2-|$\overrightarrow{a}$||$\overrightarrow{b}$|cos60°-6|$\overrightarrow{b}$|2
=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$|-96
=-72,
∴|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$|-24=0,
即(|$\overrightarrow{a}$|-6)•(|$\overrightarrow{a}$|+4)=0;
解得|$\overrightarrow{a}$|=6,
∴向量$\overrightarrow{a}$的模为6.
故选:C.
点评 本题考查了平面向量数量积与夹角、模长的计算问题,是基础题目.

练习册系列答案
相关题目
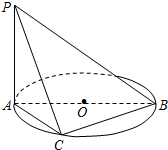 已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求:
已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求: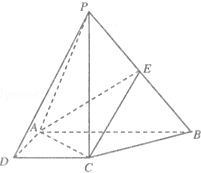 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点. 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为45°,又AC=1,BC=2PM=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为45°,又AC=1,BC=2PM=2,∠ACB=90°.