题目内容

19．直线l过点P（-1，2），且倾斜角为45°，则直线l的方程为（　　）
A．x-y+1=0B．x-y-1=0C．x-y-3=0D．x-y+3=0

分析 根据直线的倾斜角求出斜率k，用点斜式写出直线方程，再化为一般式即可．

解答 解：直线l过点P（-1，2），且倾斜角为45°，
则直线l的斜率为k=tan45°=1，
直线方程为y-2=1×（x+1），
即x-y+3=0．
故选：D．

点评 本题考查了直线的倾斜角与斜率以及点斜式方程和一般式方程的应用问题，是基础题目．

练习册系列答案
相关题目
7．抛物线y2=2px的焦点为F，过点F斜率为k的直线交抛物线于A，B两点，以AB为直径的圆与直线k：x=-2相切，则p的值为（　　）
A．2B．4C．6D．由k的值确定
8．已知函数f（x）=-log3（9x）•log3$\frac{x}{3}$（$\frac{1}{9}$≤x≤27）．
（1）设t=log3x，求t的取值范围
（2）求f（x）的最小值，并指出f（x）取得最小值时x的值．
7．证明不等式：a，b，c∈R，a4+b4+c4≥abc（a+b+c）．
14．学校体育队共有5人，其中会打排球的有2人，会打乒乓球的有5人，现从中选2人．设ξ为选出的人中既会打排球又会打乒乓球的人数，则随机变量ξ的均值E（ξ）=（　　）
A．$\frac{2}{5}$B．$\frac{3}{5}$C．$\frac{4}{5}$D．1
4．在向南方雪灾受灾地区的捐款活动中，某慈善组织收到一笔10000元的匿名捐款，该组织经过调查，发现是甲、乙、丙、丁四个人当中的某一个捐的．慈善组织成员对他们进行求证时，发现他们的说法互相矛盾．
甲说：对不起，这钱不是我捐的
乙说：我估计这钱肯定是丁捐的
丙说：乙的收入最高，肯定是乙捐的
丁说：乙的说法没有任何根据
假定四人中只有一个说了真话，那么真正的捐款者是甲（仅一人）．
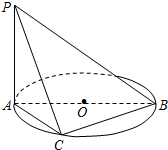11．已知PA垂直于以AB为直径的ΘO所在的平面，C是ΘO上异于A，B的动点，PA=1，AB=2，当三棱锥P-ABC取得最大体积时，求：
（1）PC与AB所成角的大小；
（2）PA与面PCB所成角的大小．
8．计算C${\;}_{n}^{1}$+2•C${\;}_{n}^{2}$2+…+n•C${\;}_{n}^{n}$2n-1=n（1+2）n-1，可以采用以下方法：
构造恒等式：C${\;}_{n}^{0}$+C${\;}_{n}^{1}$2x+C${\;}_{n}^{2}$22x2+…+C${\;}_{n}^{n}$2nxn=（1+2x）n
两边对x导，得C${\;}_{n}^{1}$2+2•C${\;}_{n}^{2}$22x+••+n•C${\;}_{n}^{n}$2nxn-1=2n（1+2x）n-1
在上式中令x=1，得C${\;}_{n}^{1}$+2•C${\;}_{n}^{2}$2+…+n•C${\;}_{n}^{n}$2n-1=n（1+2）n-1=n•3n-1，
类比上述计算方法，计算C${\;}_{n}^{1}$2+22C${\;}_{n}^{2}$22+32C${\;}_{n}^{3}$23+…+n2C${\;}_{n}^{n}$2n=2n（2n+1）3n-2．
9．已知向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=2|$\overrightarrow b$|≠0，且函数在f（x）=$\frac{1}{3}{x^3}+\frac{1}{2}|\overrightarrow a|{x^2}$$+（\overrightarrow a•\overrightarrow b）x$在R上有极值，则向量$\overrightarrow a$，$\overrightarrow b$的夹角的取值范围是（$\frac{π}{3}$，π）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网