题目内容
13.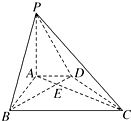 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.(1)求证:BD⊥平面PAC;
(2)求平面PBD与平面BDA的夹角.
分析 (1)分别以AB、AD、AP所在直线为x、y、z轴,建立如图所示的空间直角坐标系,利用向量法能证明BD⊥平面PAC.
(2)求出平面BDP的法向量和平面ABD的法向量,利用向量法能求出平面PBD与平面BDA的夹角.
解答 证明:(1)∵在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,
∴由题可知,AP、AD、AB两两垂直,
分别以AB、AD、AP所在直线为x、y、z轴,建立如图所示的空间直角坐标系,
则A(0,0,0),B($\sqrt{3}$,0,0),C(2$\sqrt{3}$,6,0),D(0,2,0),P(0,0,3),
$\overrightarrow{AP}$=(0,0,3),$\overrightarrow{AC}$=(2$\sqrt{3}$,6,0),$\overrightarrow{BD}$=(-2$\sqrt{3}$,2,0),
∴$\overrightarrow{BD}•\overrightarrow{AP}$=0,$\overrightarrow{BD}•\overrightarrow{AC}$=0,
∴BD⊥AP,BD⊥AC,
又PA∩AC=A,∴BD⊥平面PAC,
解:(2)设平面BDP的法向量$\overrightarrow{n}$=(x,y,z),
∵$\overrightarrow{BD}$=(-2$\sqrt{3}$,2,0),$\overrightarrow{BP}$=(-2$\sqrt{3}$,0,3),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=-2\sqrt{3}x+2y=0}\\{\overrightarrow{n}•\overrightarrow{BP}=-2\sqrt{3}x+3z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},3,2$),
平面ABD的法向量$\overrightarrow{m}$=(0,0,1),
设平面PBD与平面BDA的夹角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{16}}$=$\frac{1}{2}$,∴θ=60°,
∴平面PBD与平面BDA的夹角为60°.
点评 本题考查线面垂直的证明,考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

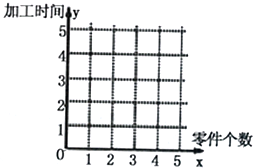 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+a,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?参考公式:
b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
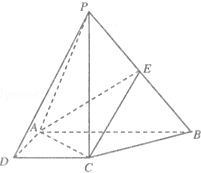 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.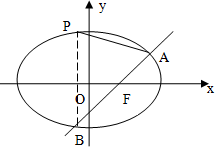 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的离心率为$e=\frac{1}{2}$,直线x+2y-1=0经过椭圆的一个焦点;
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的离心率为$e=\frac{1}{2}$,直线x+2y-1=0经过椭圆的一个焦点;