题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，若A=120°，B=45°，a=
，则b=（ ）
| 2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：正弦定理
专题：计算题,解三角形
分析：利用正弦定理，把已知条件代入即可．
解答：
解：由正弦定理得
=
，
∴b=
•sinB=
×
=
，
故选：B．
| a |
| sinA |
| b |
| sinB |
∴b=
| a |
| sinA |
| ||||
|
| ||
| 2 |
2
| ||
| 3 |
故选：B．
点评：本题主要考查了正弦定理的运用．注重了学生基础知识的考查．
练习册系列答案
相关题目
下列命题中，m，n表示两条不同的直线，α，β，γ表示三个不同的平面，正确的命题是（ ）
①若m⊥α，n∥α，则m⊥n ②若α⊥γ，β∥γ，则α∥β
③若m∥α，n∥α，则m∥n ④若α∥β，β∥γ，m⊥α，则m⊥γ
①若m⊥α，n∥α，则m⊥n ②若α⊥γ，β∥γ，则α∥β
③若m∥α，n∥α，则m∥n ④若α∥β，β∥γ，m⊥α，则m⊥γ
| A、①③ | B、②③ | C、①④ | D、②④ |
有50件产品，编号为00，01，02，03，…，49．现从中抽取5件进行检验，用系统抽样方法所抽取样本的编号可以是（ ）
| A、05，10，15，20，25 |
| B、05，14，22，30，38 |
| C、08，22，23，31，40 |
| D、00，10，20，30，40 |
已知i为虚数单位，复数z满足zi=（
）2，则复数z的共轭复数在复平面内对应的点位于（ ）
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知三角形ABC的三个内角A﹑B﹑C对边分别为a﹑b﹑c，则下列数值中，一定能构成三角形的三边的是（ ）
| A、a2﹑b2﹑c2 | ||||||||
B、
| ||||||||
C、1+
| ||||||||
| D、sinA﹑sinB﹑sinC |
若集合A={0，2，3，5}，则集合A的真子集共有（ ）
| A、7个 | B、8个 |
| C、15个 | D、16个 |
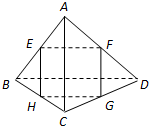如图，空间四边形ABCD中，E，F，G，H分别为BA，AD，DC，CB边上的中点．则下列说法中不正确的是（ ）| A、四边形EFGH为平行四边形 |
| B、直线AC∥平面EFGH |
| C、若棱AC=BD，则四边形EFGH为矩形 |
| D、若棱AC=BD，则四边形EFGH为菱形 |