题目内容
已知函数f（x）=-x2，则（ ）
| A、f（x）在（-∞，0）上是减函数 |
| B、f（x）是减函数 |
| C、f（x）是增函数 |
| D、f（x）在（-∞，0）上是增函数 |
考点：二次函数的性质
专题：函数的性质及应用
分析：通过函数的解析式读出函数的开口方向，和对称轴，从而得出答案．
解答：
解：∵f（x）=-x2，
开口向下，对称轴x=0，
∴f（x）在（-∞，0）递增，在（0，+∞）递减，
故选：D．
开口向下，对称轴x=0，
∴f（x）在（-∞，0）递增，在（0，+∞）递减，
故选：D．
点评：本题考查了二次函数的性质问题，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图是函数f（x）的导函数f′（x）的图象，则下面判断正确的是（ ）
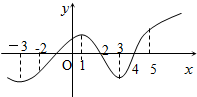
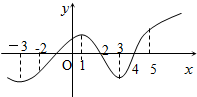
| A、函数f（x）在区间（-2，1）上单调递增 |
| B、函数f（x）在x=1处取得极大值 |
| C、函数f（x）在（4，5）上单调递增 |
| D、当x=4时，f（x）取极大值 |
已知点P是抛物线y2=4x上的一点，设点P到此抛物线的准线的距离为d1，到直线x-2y+10=0的距离为d2，则d1+d2的最小值为（ ）
A、
| ||||
| B、4 | ||||
| C、5 | ||||
D、
|
设函数f（x）=ax，（a＞0，a≠1），f（2）=4，则（ ）
| A、f（-2）＞f（-1） |
| B、f（1）＞f（2） |
| C、f（-2）＞f（2） |
| D、f（-1）＞f（-2） |