题目内容
17.若直线ax+by-1=0平分圆x2+y2-4x-4y-8=0的周长,则 ab的最大值为$\frac{1}{16}$.分析 把圆的方程化为标准形式,求出圆心和半径,把圆心坐标代入直线ax+by-1=0,利用基本不等式求出ab的最大值.
解答 解:圆x2+y2-4x-4y-8=0 即(x-2)2 +(y-2)2=16,表示圆心在(2,2),半径等于4的圆
∵直线ax+by-1=0平分圆x2+y2-4x-4y-8=0的周长,
∴直线ax+by-1=0过圆C的圆心(2,2),
∴有2a+2b=1,
∴a,b同为正时,2a+2b=1≥$2\sqrt{4ab}$,
∴ab≤$\frac{1}{16}$,
∴ab的最大值为$\frac{1}{16}$,
故答案为$\frac{1}{16}$.
点评 本题考查直线和圆的位置关系,基本不等式的应用,判断圆心(2,2)在直线ax+by-1=0上是解题的关键,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
10.执行如图所示的程序框图,若输出S的值为0.99,则判断框内可填入的条件是( )
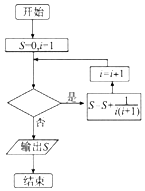

| A. | i<100 | B. | i≤100 | C. | i<99 | D. | i≤98 |
2.等比数列{an}中,a2=4,a6和a2的等比中项等于±6,则a6=( )
| A. | 9 | B. | -9 | C. | ±8 | D. | 8 |
7.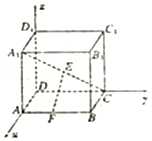 如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
 如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )| A. | $\sqrt{2}a$ | B. | $\frac{{\sqrt{2}}}{2}a$ | C. | a | D. | $\frac{1}{2}a$ |