题目内容
已知函数A={x|y=cos（
）}，B={y|y=tanx，x∈[-
，
]}，则A∩B=（ ）
| 1 |
| x+1 |
| π |
| 4 |
| π |
| 4 |
| A、∅ |
| B、{x|x≠-1} |
| C、{x|-1≤x≤1} |
| D、{x|-1＜x≤1} |
考点：交集及其运算
专题：集合
分析：先由三角函数的性质，分别求出集合A和B，再由交集的定义求A∩B．
解答：
解：∵函数A={x|y=cos（
）}={x|x≠-1}，
B={y|y=tanx，x∈[-
，
]}={y|-1≤y≤1}，
∴A∩B={x|1＜x≤1}．
故选：D．
| 1 |
| x+1 |
B={y|y=tanx，x∈[-
| π |
| 4 |
| π |
| 4 |
∴A∩B={x|1＜x≤1}．
故选：D．
点评：本题考查集合的交集的求法，是基础题，解题时要认真审题，注意三角函数的性质和交集性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
设a，b是两条不同的直线，α，β是两个不同的平面，a?α，b⊥β，则α∥β是a⊥b的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
若集合A={x|x（x-4）≤0}，B={x|log2（x2-x）＞1}，则A∩B=（ ）
| A、（2，4] |
| B、[2，4] |
| C、（-∞，0）∪[0，4] |
| D、（-∞，-1）∪[0，4] |
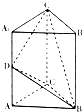如图，在直三棱柱ABC-A1B1C1中，AC=BC=