题目内容

若集合A={x|x（x-4）≤0}，B={x|log2（x2-x）＞1}，则A∩B=（　　）
A、（2，4]
B、[2，4]
C、（-∞，0）∪[0，4]
D、（-∞，-1）∪[0，4]
考点：交集及其运算
专题：集合
分析：求出集合A，B，利用集合的基本运算进行求解．
解答： 解：A={x|x（x-4）≤0}={x|0≤x≤4}，
B={x|log2（x2-x）＞1}={x|x2-x＞2}={x|x＞2或x＜-1}，
则A∩B={x|2＜x≤4}，
故选：A
点评：本题主要考查集合的基本运算，要求熟练掌握集合的交并补运算，比较基础．
练习册系列答案
相关题目
下列说法中正确的是（　　）
①若一个平面内的任何直线都与另一个平面无公共点，则这两个平面平行；
②过平面外一点有且仅有一个平面和已知平面平行；
③过平面外两点不能作平面与已知平面平行；
④若一条直线和一个平面平行，经过这条直线的任何平面都与已知平面平行．
A、①③B、②④C、①②D、③④
求y=logasin2x（a＞0且a≠1）的导数．
化简：
（1）
sin(α-π)cot(α-2π)
cos(α-π)tan(α-2π)
．
（2）cot2α（tan2α-sin2α）．
已知函数A={x|y=cos（
1
x+1
）}，B={y|y=tanx，x∈[-
π
4
，
π
4
]}，则A∩B=（　　）
A、∅
B、{x|x≠-1}
C、{x|-1≤x≤1}
D、{x|-1＜x≤1}
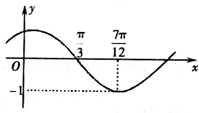函数f（x）=Asin（ωx+φ）（其中A＞0，ω，0，|φ|＜
π
2
）的图象如图所示，为了得到g（x）=sin2x的图象，则只需将f（x）的图象（　　）
A、向左平移
π
6
个长度单位
B、向右平移
π
3
个长度单位
C、向右平移
π
6
个长度单位
D、向左平移
π
3
个长度单位
某几何体的三视图如图，则该几何体的表面积为（　　）
A、24B、36C、48D、60
已知
a
，
b
，
c
是同一平面内的三个向量，其中
a
=（1，-2）
（1）若|
b
|=2
5
，且
a
与
b
同向，求
b
的坐标
（2）若|
c
|=
15
，且
a
与
c
的夹角为30°，求（2
a
+
c
）•（4
a
-3
c
）
已知函数f（x）=x3+ax2+4（a∈R是常数），曲线y=f（x）在点（1，f（1））处的切线在y轴上的截距为5．
（1）求a的值；
（2）k≤0，讨论直线y=kx与曲线y=f（x）的公共点的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网