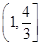题目内容
已知抛物线 上存在关于直线
上存在关于直线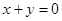 对称的相异两点
对称的相异两点 ,则
,则 等于( )
等于( )
| A.3 | B.4 | C. | D. |
C
解析试题分析:设 ,因为
,因为 关于直线
关于直线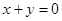 对称,所以
对称,所以 .又
.又 在抛物线
在抛物线 上,所以
上,所以
 ,化简得
,化简得
所以 或
或 或
或 .当
.当 时,
时,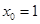 ,即
,即 、
、 ,此时
,此时 ;
;
当 时,
时, ,即
,即 、
、 ,此时
,此时 ;
;
当 时,
时,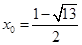 ,即
,即 、
、 ,此时
,此时 为同一点.与题意矛盾;
为同一点.与题意矛盾;
当 时,
时, ,即
,即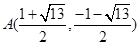 、
、 ,此时
,此时 为同一点.与题意矛盾.综上所述,
为同一点.与题意矛盾.综上所述, .
.
考点:直线与抛物线的位置关系

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果点 在以点
在以点 为焦点的抛物线
为焦点的抛物线 上,则
上,则 ( )
( )
A. | B. | C. | D. |
椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A. | B. | C.2 | D.4 |
已知椭圆 和双曲线
和双曲线 有公共的焦点,那么双曲线的渐近线方程为
有公共的焦点,那么双曲线的渐近线方程为
A. | B. | C. | D. |
已知抛物线 的焦点与双曲线
的焦点与双曲线 的一个焦点重合,则该双曲线的离心率为( )
的一个焦点重合,则该双曲线的离心率为( )
A. | B. | C. | D. |

 ,过其焦点且斜率为-1的直线交抛物线于
,过其焦点且斜率为-1的直线交抛物线于 两点,若线段
两点,若线段 的中点的纵坐标为-2,则该抛物线的准线方程为( )
的中点的纵坐标为-2,则该抛物线的准线方程为( )



 ,过其焦点且斜率为1的直线交抛物线与A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为( )
,过其焦点且斜率为1的直线交抛物线与A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为( ) B.
B. C.
C. D.
D.
 上任意一点
上任意一点 ,作与实轴平行的直线,交两渐近线于
,作与实轴平行的直线,交两渐近线于 、
、 两点,若
两点,若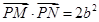 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )



 左支上的一点,其右焦点为
左支上的一点,其右焦点为 ,若
,若 为线段
为线段 的中点, 且
的中点, 且 ,则双曲线的离心率
,则双曲线的离心率 的取值范围是 ( )
的取值范围是 ( )