题目内容
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且在点Pn(n,Sn)处的切线的斜率为kn.
(1) 求数列{an}的通项公式;
(2) 若bn=2knan,求数列{bn}的前n项和Tn.
解: (1) ∵ 点Pn(n,Sn)在函数f(x)=x2+2x的图象上,
∴ Sn=n2+2n(n∈N*),当n≥2时,an=Sn-Sn-1=2n+1,当n=1时,a1=S1=3满足上式,所以数列{an}的通项公式为an=2n+1.
(2) 由f(x)=x2+2x,求导得f′(x)=2x+2.
∵ 在点Pn(n,Sn)处的切线的斜率为kn,
∴ kn=2n+2,∴ bn=2knan=4·(2n+1)·4n,
∴ Tn=4×3×4+4×5×42+4×7×43+…+4×(2n+1)×4n,
用错位相减法可求得Tn= ·4n+2-
·4n+2- .
.

练习册系列答案
相关题目
 ,则{an}的前10项和为________.
,则{an}的前10项和为________.
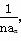 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. =________.
=________. 的等比数列,则其最大角的余弦值为________.
的等比数列,则其最大角的余弦值为________.