题目内容
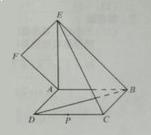
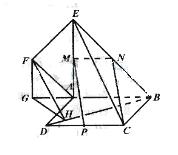
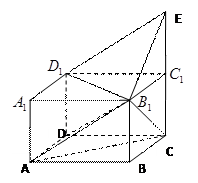
(本小题满分12分)如图,正方形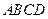 所在平面与平面四边形
所在平面与平面四边形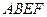 所在平面互相垂直,△
所在平面互相垂直,△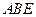 是等腰直角三角形,
是等腰直角三角形,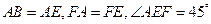 。
。
(Ⅰ)求证: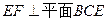 ;
;
(Ⅱ)设线段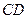 的中点为
的中点为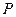 ,在直线
,在直线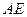 上是否存在一点
上是否存在一点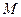 ,使得
,使得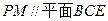 ?若存在,请指出点
?若存在,请指出点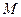 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
(Ⅲ)求二面角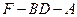 的大小。
的大小。
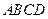 所在平面与平面四边形
所在平面与平面四边形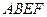 所在平面互相垂直,△
所在平面互相垂直,△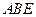 是等腰直角三角形,
是等腰直角三角形,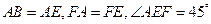 。
。
(Ⅰ)求证:
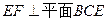 ;
;(Ⅱ)设线段
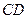 的中点为
的中点为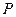 ,在直线
,在直线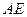 上是否存在一点
上是否存在一点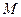 ,使得
,使得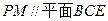 ?若存在,请指出点
?若存在,请指出点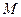 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;(Ⅲ)求二面角
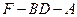 的大小。
的大小。(Ⅰ)证明见解析。
(Ⅱ)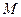 为线段AE的中点,证明见解析。
为线段AE的中点,证明见解析。
(Ⅲ)arctan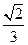
(Ⅱ)
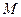 为线段AE的中点,证明见解析。
为线段AE的中点,证明见解析。(Ⅲ)arctan
本小题主要考查平面与平面垂直、直线与平面垂直、直线与平面平行、二面角等基础知识,考查空间想象能力、逻辑推理能力和数学探究意识,考查应用向量知识解决数学问题的能力。
解法一:
(Ⅰ)因为平面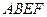 ⊥平面
⊥平面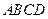 ,
,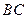
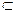 平面
平面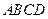 ,
,
平面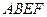
 平面
平面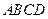
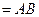 ,
,
所以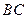 ⊥平面
⊥平面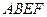
所以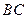 ⊥
⊥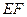 。
。
因为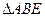 为等腰直角三角形,
为等腰直角三角形,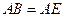 ,
,
所以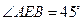
又因为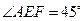 ,
,
所以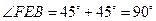 ,
,
即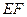 ⊥
⊥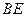
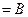 ,
,
所以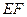 ⊥平面
⊥平面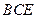 。………………………………4分
。………………………………4分
(Ⅱ)存在点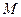 ,当
,当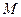 为线段AE的中点时,PM∥平面
为线段AE的中点时,PM∥平面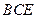
取BE的中点N,连接AN,MN,则MN∥=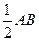 ∥=PC
∥=PC
所以PMNC为平行四边形,所以PM∥CN
因为CN在平面BCE内,PM不在平面BCE内,
所以PM∥平面BCE………………………………8分
(Ⅲ)由EA⊥AB,平面ABEF⊥平面ABCD,易知,EA⊥平面ABCD
作FG⊥AB,交BA的延长线于G,则FG∥EA。从而,FG⊥平面ABCD
作GH⊥BD于G,连结FH,则由三垂线定理知,BD⊥FH
因此,∠AEF为二面角F-BD-A的平面角
因为FA="FE," ∠AEF=45°,
所以∠AFE=90°,∠FAG=45°.
设AB=1,则AE=1,AF=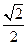 。
。
FG=AF·sinFAG=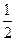
在Rt△FGH中,∠GBH=45°,BG=AB+AG=1+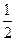 =
=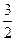 ,
,
GH=BG·sinGBH=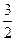 ·
·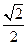 =
=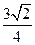
在Rt△FGH中,tanFHG=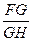 =
= 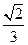
故二面角F-BD-A的大小为arctan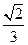 ……………………………12分
……………………………12分
解法二:
(Ⅰ)因为△ABE为等腰直角三角形,AB=AE,
所以AE⊥AB.
又因为平面ABEF⊥平面ABCD,AE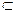 平面ABEF,
平面ABEF,
平面ABEF∩平面ABCD=AB,
所以AE⊥平面ABCD.
所以AE⊥AD.
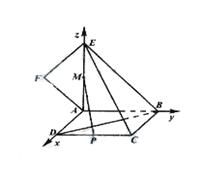
因此,AD,AB,AE两两垂直,以A为坐标原点,建立如图所示的直角坐标系A-xyz.
设AB=1,则AE=1,B(0,1,0),D (1, 0, 0 ) ,
E ( 0, 0, 1 ), C ( 1, 1, 0 ).
因为FA="FE," ∠AEF = 45°,
所以∠AFE= 90°.
从而,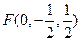 .
.
所以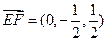 ,
,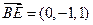 ,
,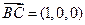 .
.
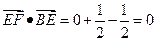 ,
,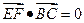 .
.
所以EF⊥BE, EF⊥BC.
因为BE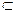 平面BCE,BC∩BE="B" ,
平面BCE,BC∩BE="B" ,
所以EF⊥平面BCE.
(Ⅱ) M(0,0,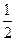 ).P(1,
).P(1, 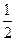 ,0).
,0).
从而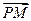 =(
=(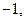
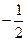 ,
,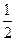 ).
).
于是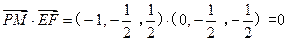
所以PM⊥FE,又EF⊥平面BCE,直线PM不在平面BCE内,
故PM∥平面BCE………………………………8分
(Ⅲ) 设平面BDF的一个法向量为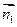 ,并设
,并设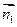 =(x,y,z)
=(x,y,z)
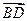 =(1,
=(1,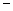 1,0),
1,0),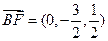
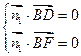 即
即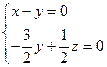
去y=1,则x=1,z=3,从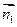 =(0,0,3)
=(0,0,3)
取平面ABD的一个法向量为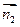 =(0,0,1)
=(0,0,1)
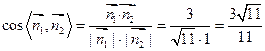
故二面角F-BD-A的大小为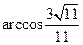 ……………………………………12分
……………………………………12分
解法一:

(Ⅰ)因为平面
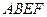 ⊥平面
⊥平面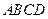 ,
,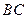
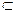 平面
平面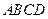 ,
,平面
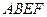
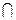 平面
平面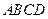
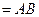 ,
,所以
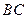 ⊥平面
⊥平面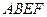
所以
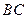 ⊥
⊥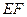 。
。因为
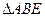 为等腰直角三角形,
为等腰直角三角形,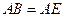 ,
,所以
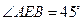
又因为
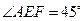 ,
,所以
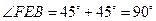 ,
,即
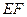 ⊥
⊥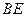
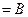 ,
,所以
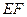 ⊥平面
⊥平面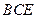 。………………………………4分
。………………………………4分(Ⅱ)存在点
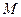 ,当
,当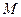 为线段AE的中点时,PM∥平面
为线段AE的中点时,PM∥平面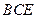
取BE的中点N,连接AN,MN,则MN∥=
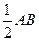 ∥=PC
∥=PC所以PMNC为平行四边形,所以PM∥CN
因为CN在平面BCE内,PM不在平面BCE内,
所以PM∥平面BCE………………………………8分
(Ⅲ)由EA⊥AB,平面ABEF⊥平面ABCD,易知,EA⊥平面ABCD
作FG⊥AB,交BA的延长线于G,则FG∥EA。从而,FG⊥平面ABCD
作GH⊥BD于G,连结FH,则由三垂线定理知,BD⊥FH
因此,∠AEF为二面角F-BD-A的平面角
因为FA="FE," ∠AEF=45°,
所以∠AFE=90°,∠FAG=45°.
设AB=1,则AE=1,AF=
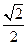 。
。FG=AF·sinFAG=
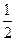
在Rt△FGH中,∠GBH=45°,BG=AB+AG=1+
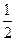 =
=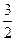 ,
,GH=BG·sinGBH=
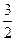 ·
·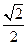 =
=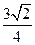
在Rt△FGH中,tanFHG=
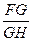 =
= 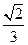
故二面角F-BD-A的大小为arctan
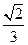 ……………………………12分
……………………………12分解法二:

(Ⅰ)因为△ABE为等腰直角三角形,AB=AE,
所以AE⊥AB.
又因为平面ABEF⊥平面ABCD,AE
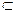 平面ABEF,
平面ABEF,平面ABEF∩平面ABCD=AB,
所以AE⊥平面ABCD.
所以AE⊥AD.
因此,AD,AB,AE两两垂直,以A为坐标原点,建立如图所示的直角坐标系A-xyz.
设AB=1,则AE=1,B(0,1,0),D (1, 0, 0 ) ,
E ( 0, 0, 1 ), C ( 1, 1, 0 ).
因为FA="FE," ∠AEF = 45°,
所以∠AFE= 90°.
从而,
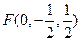 .
.所以
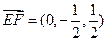 ,
,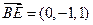 ,
,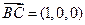 .
.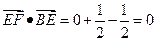 ,
,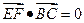 .
.所以EF⊥BE, EF⊥BC.
因为BE
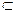 平面BCE,BC∩BE="B" ,
平面BCE,BC∩BE="B" ,所以EF⊥平面BCE.
(Ⅱ) M(0,0,
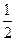 ).P(1,
).P(1, 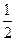 ,0).
,0).从而
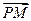 =(
=(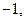
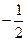 ,
,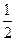 ).
).于是
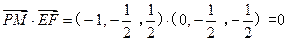
所以PM⊥FE,又EF⊥平面BCE,直线PM不在平面BCE内,
故PM∥平面BCE………………………………8分
(Ⅲ) 设平面BDF的一个法向量为
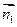 ,并设
,并设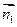 =(x,y,z)
=(x,y,z)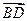 =(1,
=(1,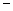 1,0),
1,0),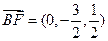
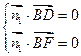 即
即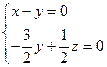
去y=1,则x=1,z=3,从
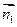 =(0,0,3)
=(0,0,3)取平面ABD的一个法向量为
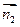 =(0,0,1)
=(0,0,1)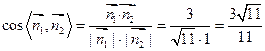
故二面角F-BD-A的大小为
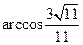 ……………………………………12分
……………………………………12分
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
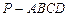 中,底面
中,底面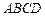 是一直角梯形,
是一直角梯形,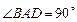 ,
,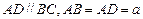 ,
,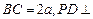 底面
底面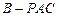 的体积;
的体积;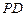 上是否存在一点
上是否存在一点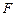 ,使得
,使得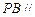 平面
平面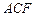 ,若存在,求出
,若存在,求出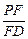 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
 ,EF=EC=1,
,EF=EC=1, 
 平面BCD;
平面BCD;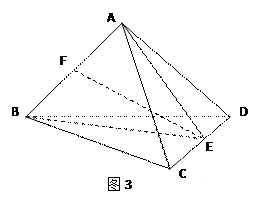
 中,点
中,点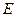 在棱
在棱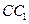 的延长线上,
的延长线上,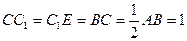 .
.
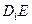 //平面
//平面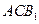 ;
; (Ⅱ) 求证:平面
(Ⅱ) 求证:平面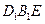
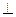 平面
平面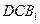 ;
;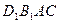 的体积.
的体积.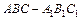 中,
中,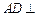 平面
平面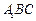 ,其垂足
,其垂足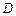 落在直线
落在直线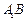 上.
上.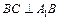 ;
;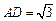 ,
,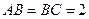 ,
,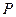 为
为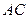 的中点,求三棱锥
的中点,求三棱锥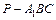 的体积.
的体积.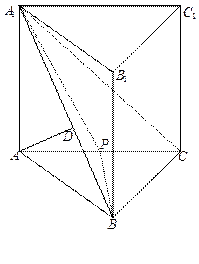
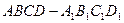 的底面ABCD是菱形,且
的底面ABCD是菱形,且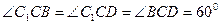 ,(1)证明:
,(1)证明: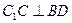 ;
;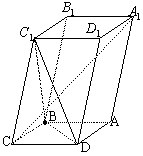
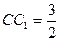 ,记面
,记面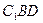 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;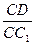 的值为多少时,能使
的值为多少时,能使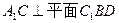 ?请给出证明.
?请给出证明. 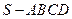 的底面是正方形,
的底面是正方形,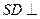 平面
平面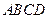 .
.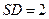 ,
,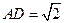 ,
,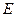 是
是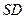 上的点.
上的点.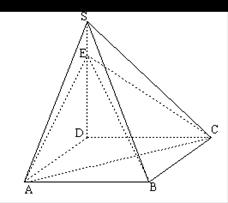
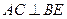 ;
;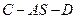 的余弦值.
的余弦值.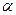 ⊥平面
⊥平面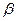 ,那么
,那么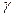 ,平面
,平面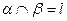 ,那么
,那么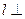 平面
平面