题目内容

17．若实数x，y满足|x|-ln $\frac{1}{y}$=0，则y关于x的函数的图象形状大致是（　　）
A．B．C．D．

分析 由条件可得 y=$\frac{1}{{e}^{\left|x\right|}}$，显然定义域为R，且过点（0，1），当x＞0时，y=$\frac{1}{{e}^{x}}$，是减函数，从而得出结论

解答 解：若变量x，y满足|x|-ln $\frac{1}{y}$=0，
则得 y=$\frac{1}{{e}^{\left|x\right|}}$，显然定义域为R，且过点（0，1），故排除C、D．
再由当x＞0时，y=$\frac{1}{{e}^{x}}$，是减函数，故排除A，
故选B

点评 本题主要考查指数式与对数式的互化，指数函数的图象和性质的综合应用，以及函数的定义域、值域、单调性、函数图象过定点问题，属于中档题．

练习册系列答案
相关题目
7．设命题p：方程x2+y2-2x-4y+m=0表示的曲线是一个圆；
命题q：方程$\frac{{x}^{2}}{m-6}$-$\frac{{y}^{2}}{m+3}$=1所表示的曲线是双曲线，若“p∧q”为假，求实数m的取值范围．
8．某四棱锥的三视图如图所示，则俯视图的面积为（　　）
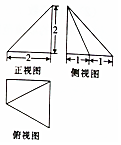
A．2B．$\frac{5}{2}$C．3D．4
5．幂函数f（x）=（m2-2m+1）x2m-1在（0，+∞）上为增函数，则实数m的值为（　　）
A．0B．1C．2D．1或2
12．设集合A={x|a-1＜x＜a+1}，B={x|x＜-1或x＞2}．
（1）若A∩B=∅，求实数a的取值范围；
（2）若A∪B=B，求实数a的取值范围．
2．某企业第三年的产量比第一年的产量增加44%，若每年的平均增长率相同（设为x），则以下结论正确的是（　　）
A．x＞22%B．x＜22%C．x=22%D．以上都不对
9．已知tan（$\frac{π}{4}$+α）=$\frac{1}{2}$，则tanα的值为（　　）
A．-$\frac{1}{3}$B．$\frac{1}{3}$C．-$\frac{1}{2}$D．-1
6．设向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=2\sqrt{2}，|{\overrightarrow b}|=\sqrt{2}$，且$\overrightarrow a•\overrightarrow b=1$，则$|{\overrightarrow a-2\overrightarrow b}|$=（　　）
A．$2\sqrt{3}$B．12C．$2\sqrt{2}$D．8
16．设m、n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题：
①若m∥n，n?α，则m∥α 
②若m⊥α，m∥β，则α⊥β
③α∥β，α∥γ，则β∥γ      
④若α⊥β，m∥α，则m⊥β
其中正确命题的序号是（　　）
A．①③B．①④C．②③D．②④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网