题目内容
已知x>0,y>0,x+2y-2xy=0,则x+2y的最小值是 .
考点:基本不等式
专题:不等式的解法及应用
分析:利用基本不等式与一元二次不等式的解法即可得出.
解答:
解:∵x>0,y>0,x+2y-2xy=0,
∴x+2y=x•2y≤(
)2,
解得x+2y≥4,当且仅当x=2y=2时取等号.
∴x+2y的最小值是4.
故答案为:4.
∴x+2y=x•2y≤(
| x+2y |
| 2 |
解得x+2y≥4,当且仅当x=2y=2时取等号.
∴x+2y的最小值是4.
故答案为:4.
点评:本题考查了基本不等式与一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
已知f(x)=xcosx,则f′(x)=( )
| A、cosx-xsinx |
| B、cosx+xsinx |
| C、sinx-xcosx |
| D、sinx+xcosx |
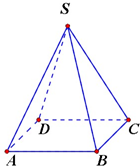 若正四棱锥底面边长为a,侧棱与底面成60°角,求:
若正四棱锥底面边长为a,侧棱与底面成60°角,求: