题目内容

若正四棱锥底面边长为a，侧棱与底面成60°角，求：
（1）棱锥的侧棱和斜高；
（2）棱锥的侧面和底面所成的角．
考点：二面角的平面角及求法,棱锥的结构特征
专题：空间位置关系与距离,空间角
分析：（1）在正四棱锥SABCD中，SO⊥底面ABCD，则O是底面中心，∠SBO=60°，从而SB=2OB=
2
a，作OM⊥BC于M，连结SM，则SM⊥BC，由此能求出棱锥的侧棱和斜高．
（2）∠SMO即为侧面与底面所成的角，由此能求出棱锥的侧面和底面所成的角．
解答： 解：（1）如图所示，在正四棱锥SABCD中，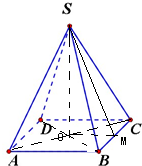
SO⊥底面ABCD，则O是底面中心，
∠SBO即为侧棱SB与底面ABCD所成的角，
故∠SBO=60°，
∴SB=2OB=
2
a，
作OM⊥BC于M，连结SM，则SM⊥BC，
∴SM即为正四棱锥的斜高，
在Rt△SOM中，SM=
7
2
a．
∴正四棱锥的侧棱长为
2
a，斜高为
7
2
a．
（2）由（1）知，∠SMO即为侧面与底面所成的角，
cos∠SMO=
1
2
a
7
2
a
=
7
7
．
∴∠SMO=arccos 
7
7
，
即棱锥的侧面和底面所成的角为arccos 
7
7
．
点评：本题考查棱锥的侧棱和斜高的求法，考查棱锥的侧面和底面所成的角的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
某食品加工厂甲，乙两个车间包装小食品，在自动包装传送带上每隔30分钟抽取一袋食品，称其重量并将数据记录如下：
甲：102  100  98  97  103  101  99
乙：102  101  99  98  103  98   99
（1）食品厂采用的是什么抽样方法（不必说明理由）？
（2）根据数据估计这两个车间所包装产品每袋的平均质量；
（3）分析哪个车间的技术水平更好些？
附：S=
1
n
[(x1-
.
x
)2+(x2-
.
x
)2+…+(xn-
.
x
)n]
．
已知三点A（1，3），B（5，11），C（-3，-5），求证：这三点在同一条直线上．
化简：
（1）
tan(π-α)•sin2(α+
π
2
)•cos(2π-α)
cos3(-π-α)•tan(α-2π)
；
（2）
sin2x
sinx-cosx
-
sinx+cosx
tan2x-1
．
已知a≠0，函数y=-acos2x-
3
asin2x+2a+b，x∈[0，
π
2
]，若函数值域为[-5，1]，求常数a，b的值．
已知正项数列{an}满足a1=
1
2
，且an+1=
an
1+an
．
（1）求证：数列{
1
an
}是等差数列；
（2）求正项数列{an}的通项公式；
（3）若等比数列{bn}的通项公式是：bn=2n-1，求数列{
bn
an
}的前n项和Sn．
若
OC
=λ
OA
+μ
OB
且λ+μ=1，则A，B，C三点共线，将这一结论类比到空间，你得到的结论是
 
．
已知f（x）=2sinx-πlnx，g（x）=2sinx-xlnx，且f（x）和g（x）的定义域都
是（0，π），下列命题：
（1）y=f（x）在其定义域上恰有一个零点；
（2）y=g（x）在其定义域上恰有一个零点；
（3）若0＜x1＜x2＜π，则f（x1）＞f（x2）；
（4）若0＜x1＜x2＜π，则g（x1）＜g（x2）．
其中正确的是
 
（把所有正确命题的序号填在答题卡的相应位置上）．
已知x＞0，y＞0，x+2y-2xy=0，则x+2y的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网