题目内容
18.设x,y满足约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a,b>0)的最大值是12,则a2+b2的最小值是( )| A. | $\frac{6}{13}$ | B. | $\frac{36}{5}$ | C. | $\frac{36}{13}$ | D. | $\frac{6}{5}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数可得2a+3b=6,再由点到直线的距离公式求得a2+b2的最小值.
解答 解:由约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0,y≥0}\end{array}\right.$作出可行域如图所示,
联立$\left\{\begin{array}{l}{x-y+2=0}\\{3x-y-6=0}\end{array}\right.$,解得A(4,6),
化目标函数z=ax+by为y=-$-\frac{a}{b}x+\frac{z}{b}$,由图可知,
当直线y=-$-\frac{a}{b}x+\frac{z}{b}$过点A(4,6)时,z有最大值为4a+6b=12.
∴2a+3b=6.
由原点O(0,0)到直线2a+3b-6=0的距离d=$\frac{|-6|}{\sqrt{{2}^{2}+{3}^{2}}}=\frac{6}{\sqrt{13}}$,
可得a2+b2的最小值是$\frac{36}{13}$.
故选:C.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
13.设i是叙述虚数单位,若复数2-$\frac{a}{2-i}$(a∈R)是纯虚数,则a的值为( )
| A. | 5 | B. | 3 | C. | -5 | D. | -3 |
3.已知复数z满足(z+1)(1+i)=1-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
7.下列函数中,以$\frac{π}{2}$为最小正周期的偶函数是( )
| A. | $y=cos({2x+\frac{π}{2}})$ | B. | y=sin22x-cos22x | C. | y=sin2x+cos2x | D. | y=sin2xcos2x |
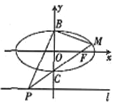 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2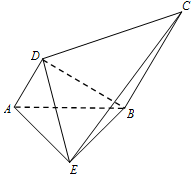 如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,
如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,