题目内容
3．已知复数z满足（z+1）（1+i）=1-i，则|z|=（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
分析 利用复数的运算法则、模的计算公式即可得出．
解答 解：∵（z+1）（1+i）=1-i，
∴z+1=$\frac{1-i}{1+i}$=$\frac{（1-i）^{2}}{（1+i）（1-i）}$=$\frac{-2i}{2}$=-i．
∴z=-1-i．
则|z|=$\sqrt{2}$．
故选：B．
点评 本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
11．
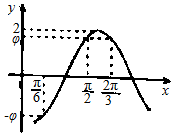已知函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列结论正确的是（ ）
已知函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列结论正确的是（ ）| A． | 函数f（x）的最小正周期为$\frac{π}{2}$ | |
| B． | 直线x=-$\frac{π}{12}$是函数f（x）图象的一条对称轴 | |
| C． | 函数f（x）在区间[-$\frac{5π}{12}$，$\frac{π}{6}$]上单调递增 | |
| D． | 将函数f（x）的图象向左平移$\frac{π}{3}$个单位，得到函数g（x）的图象，则g（x）=2sin2x |
18．设x，y满足约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0，y≥0}\end{array}\right.$，若目标函数z=ax+by（a，b＞0）的最大值是12，则a2+b2的最小值是（ ）
| A． | $\frac{6}{13}$ | B． | $\frac{36}{5}$ | C． | $\frac{36}{13}$ | D． | $\frac{6}{5}$ |
8．设f（x）=$\left\{\begin{array}{l}{3{e}^{x-1}，x＜2}\\{lo{g}_{2}（{x}^{2}-1），x≥2}\end{array}\right.$，则不等式f（x）＜3的解集为（ ）
| A． | （-∞，$\sqrt{7}$） | B． | （-∞，3） | C． | （-∞，1）∪[2，$\sqrt{7}$） | D． | （-∞，1）∪[2，3） |
15．已知△ABC是边长为4的等边三角形，D、P是△ABC内部两点，且满足$\overrightarrow{AD}=\frac{1}{4}（\overrightarrow{AB}+\overrightarrow{AC}）$，$\overrightarrow{AP}=\overrightarrow{AD}+\frac{1}{8}\overrightarrow{BC}$，则△ADP的面积为（ ）
| A． | $\frac{{\sqrt{3}}}{4}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\sqrt{3}$ |
12．球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切，点M为棱DD1的中点，则平面ACM截球O所得截面的面积为（ ）
| A． | $\frac{4π}{3}$ | B． | π | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
13．已知双曲线$\frac{x^2}{a^2}-{y^2}$=1的一条渐近线方程是y=$\frac{{\sqrt{3}}}{3}$x，则双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |