题目内容
 如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点.
如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点.(1)求直三棱柱ABC-A1B1C1的全面积;
(2)求异面直线AE与A1C所成角θ的大小(结果用反三角函数表示).
考点:异面直线及其所成的角,棱柱、棱锥、棱台的侧面积和表面积
专题:空间角
分析:(1)利用三角形的面积计算公式、矩形的面积计算公式、直棱柱的表面积计算公式即可得出;
(2)利用直角三角形的边角关系、余弦定理、异面直线所成的角即可得出.
(2)利用直角三角形的边角关系、余弦定理、异面直线所成的角即可得出.
解答:
解:(1)S△ABC=
AB•AC=
•1•1=
,
S侧=(AB+BC+AC)•AA1=(1+
+1)•2=4+2
,
∴S全=2S△ABC+S侧=5+2
.
(2)取B1C1的中点E1,连A1E1,则A1E1∥AE,即∠CA1E1即为异面直线AE与A1C所成的角θ.
连接E1C.
在Rt△E1C1C中,由E1C1=
,CC1=2
知A1C=
=
在Rt△A1C1C中,由A1C1=1,CC1=2知A1C=
,
在△A1E1C中,cosθ=
=
=
,
∴θ=arccos
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S侧=(AB+BC+AC)•AA1=(1+
| 2 |
| 2 |
∴S全=2S△ABC+S侧=5+2
| 2 |
(2)取B1C1的中点E1,连A1E1,则A1E1∥AE,即∠CA1E1即为异面直线AE与A1C所成的角θ.
连接E1C.

在Rt△E1C1C中,由E1C1=
| ||
| 2 |
知A1C=
|
3
| ||
| 2 |
在Rt△A1C1C中,由A1C1=1,CC1=2知A1C=
| 5 |
在△A1E1C中,cosθ=
(
| ||||||||||
2•
|
| 1 | ||
|
| ||
| 10 |
∴θ=arccos
| ||
| 10 |
点评:本题考查了三角形的面积计算公式、矩形的面积计算公式、直棱柱的表面积计算公式、直角三角形的边角关系、余弦定理、异面直线所成的角等基础知识与基本技能方法,考查了推理能力和实践能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
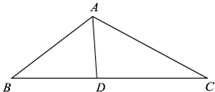 若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值(或最大值),则称此模型为“周积三角形”.某模型厂家用一根定长连接杆AD,两根单向伸缩连接杆AB、AC(A端固定,B、C端可伸缩)以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型(所有连接杆均为笔直的金属杆).模型中,双向伸缩杆BC用一个活动连接装置固定在D点,使BC可在D处自由转动.已知:模型中,∠BAD=∠CAD=60°,AD=1分米,AB和AC最多可伸长到5分米,BC的双向伸缩能力均很强.设AB=x分米,AC=y分米.
若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值(或最大值),则称此模型为“周积三角形”.某模型厂家用一根定长连接杆AD,两根单向伸缩连接杆AB、AC(A端固定,B、C端可伸缩)以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型(所有连接杆均为笔直的金属杆).模型中,双向伸缩杆BC用一个活动连接装置固定在D点,使BC可在D处自由转动.已知:模型中,∠BAD=∠CAD=60°,AD=1分米,AB和AC最多可伸长到5分米,BC的双向伸缩能力均很强.设AB=x分米,AC=y分米. 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.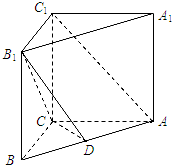 如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.