题目内容
设随机变量ξ～N（μ，σ2），且P（ξ≤c）=P（ξ＞c）=p，则p的值为：（ ）
| A、0 | B、0.5 | C、1 | D、不确定 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：根据p（ξ≤c）+p（ξ＞c）=1，可得结论．
解答：
解：随机变量ξ～N（μ，σ2），
∵p（ξ≤c）=p（ξ＞c），
p（ξ≤c）+p（ξ＞c）=1，
∴p=0.5．
故选：B．
∵p（ξ≤c）=p（ξ＞c），
p（ξ≤c）+p（ξ＞c）=1，
∴p=0.5．
故选：B．
点评：本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的性质，是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）为奇函数，且当x＞0时，f（x）=x2+
+lnx，则f（-1）=（ ）
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
函数f（x）=
的定义域是（ ）
| ||
| lg(x+1) |
| A、（0，3] |
| B、（-1，0）∪（0，3] |
| C、（-1，3] |
| D、（-1，3） |
A={x|x＞0}，B={x|x＞1}，则A∩B=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＜0} |
| D、{x|x＞1} |
为了丰富高一学生的课外生活，某校要组建数学、计算机、航空模型3个兴趣小组，小明要选报其中的2个，则基本事件有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
设（x+1）（2x+1）10=a0+a1（x+2）+a2（x+2）2+…+a11（x+2）11，则a1+a2+a3+…+a11的值是（ ）
| A、-310 |
| B、0 |
| C、310 |
| D、510 |
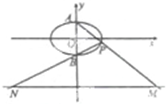如图，已知椭圆C：