题目内容
4.若两个不同平面α、β的法向量分别为$\overrightarrow{u}$=(1,2,-1),$\overrightarrow{v}$=(-2,2,2),则( )| A. | α、β相交但不垂直 | B. | α⊥β | C. | α∥β | D. | 以上均不正确 |
分析 观察两个向量坐标的数量关系,判断向量平行或垂直即可.
解答 解:∵$\overrightarrow{u}$=(1,2,-1),$\overrightarrow{v}$=(-2,2,2),
∴$\overrightarrow{u}$•$\overrightarrow{v}$=1×(-2)+2×2+(-1)×2=0,
∴$\overrightarrow{u}$⊥$\overrightarrow{v}$
∴α⊥β
故选:B.
点评 本题主要考察了空间向量的平行及垂直,是基础题.

练习册系列答案
相关题目
15.我们知道,在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足4R2=a2+b2,类比上述结论,在长方体ABCD-A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD-A1B1C1D1的外接球的半径R满足的关系式是( )
| A. | 4R2=a3+b3+c3 | B. | 8R2=a2+b2+c2 | C. | 8R3=a3+b3+c3 | D. | 4R2=a2+b2+c2 |
12.已知命题p1:函数y=ex-e-x在R为增函数,p2:函数y=ex+e-x在(0,1)为减函数.则命题p1∧p2;p1∨p2;p1∧¬p2;¬p1∨p2中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.过椭圆的右焦点F2作椭圆长轴的垂线交椭圆于A,B两点,F1为椭圆的左焦点,若△F1AB为正三角形,则椭圆的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2-$\sqrt{3}$ | D. | $\sqrt{2}$-1 |
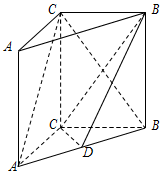 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证:
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证: