题目内容
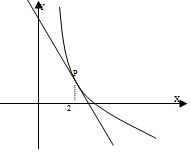
6．设i是虚数单位，复数z满足z•（1+2i）2=3+4i，则z在复平面内对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算法则、几何意义、共轭复数的定义即可得出．
解答 解：z•（1+2i）2=3+4i，∴z•（-3+4i）=3+4i，∴-z•（3-4i）（3+4i）=（3+4i）（3+4i），
∴-25z=-7+24i，可得z=$\frac{7}{25}$-$\frac{24}{25}$i．
则z在复平面内对应的点$（\frac{7}{25}，-\frac{24}{25}）$在第四象限．
故选：D．
点评 本题考查了复数的运算法则、几何意义、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
17．已知a，b，c∈（0，1），且ab+bc+ac=1，则$\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}$的最小值为（ ）
| A． | $\frac{{3-\sqrt{3}}}{2}$ | B． | $\frac{{9-\sqrt{3}}}{2}$ | C． | $\frac{{6-\sqrt{3}}}{2}$ | D． | $\frac{{9+3\sqrt{3}}}{2}$ |
1．下列语句不是命题的是（ ）
| A． | -3＞4 | B． | 0.3是整数 | C． | a＞3 | D． | 4是3的约数 |
11．
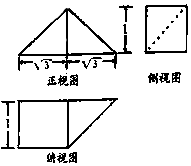《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，将底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”，已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示，则该几何体的表面积（ ）
《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，将底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”，已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示，则该几何体的表面积（ ）| A． | $4+3\sqrt{3}$ | B． | $3+3\sqrt{3}$ | C． | $4+2\sqrt{3}$ | D． | $3+4\sqrt{3}$ |
18．下列求导结果正确的是（ ）
| A． | （a-x2）′=1-2x | B． | （2$\sqrt{{x}^{3}}$）′=3$\sqrt{x}$ | C． | （cos60°）′=-sin60° | D． | [ln（2x）]′=$\frac{1}{2x}$ |
15．我们知道，在长方形ABCD中，如果设AB=a，BC=b，那么长方形ABCD的外接圆的半径R满足4R2=a2+b2，类比上述结论，在长方体ABCD-A1B1C1D1中，如果设AB=a，AD=b，AA1=c，那么长方体ABCD-A1B1C1D1的外接球的半径R满足的关系式是（ ）
| A． | 4R2=a3+b3+c3 | B． | 8R2=a2+b2+c2 | C． | 8R3=a3+b3+c3 | D． | 4R2=a2+b2+c2 |