题目内容
12.设函数f(x)=|x|x+bx+c,给出下列4个命题:①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是①②③.
分析 ①,将b的值代入,可得f(x)的解析式,进而根据函数的图象变化的规律,可得其正确;
②,将c的值代入,可得f(x)的解析式,进而由奇函数判断方法,求有f(-x)与-f(x)的关系,分析可得其正确;
③,由②可得函数f(x)=|x|x+bx的奇偶性,进行图象变化可得其正确;
④,举反例|x|x-5x+6=0有三个解-6、2、3,可得其错误.
解答 解:①当b=0,c>0时,f(x)=|x|x+c=$\left\{\begin{array}{l}{x}^{2}+c\\-{x}^{2}+c\end{array}$,结合图形知f(x)=0只有一个实数根,故①正确;
②当c=0时,f(x)=|x|x+bx,有f(-x)=-f(x)=-|x|x-bx,故y=f(x)是奇函数,故②正确;
③y=f(x)的图象可由奇函数f(x)=|x|x+bx,向上或向下平移|c|而得到,y=f(x)的图象与y轴交点为(0,c),故函数y=f(x)的图象关于(0,c)对称,故③正确;
④当b=-5,c=6时,方程|x|x-5x+6=0有三个解-6、2、3,即三个零点,故④错误;
故答案为:①②③.
点评 本题主要考查命题的真假判断,涉及函数的零点、对称性、奇偶性等知识点,注意结合函数的图象与图象的变化进行分析.

练习册系列答案
相关题目
3.若{an}是等差数列,首项a1>0,a2016+a2017>0,a2016.a2017<0,则使前n项和Sn>0成立的最大自然数n是( )
| A. | 4031 | B. | 4033 | C. | 4034 | D. | 4032 |
20.方程$\frac{{x}^{2}}{4-t}$+$\frac{{y}^{2}}{t-1}$=1表示曲线C,给出以下命题:
①曲线C不可能为圆;
②若1<t<4,则曲线C为椭圆;
③若曲线C为双曲线,则t<1或t>4;
④若曲线C为焦点在x轴上的椭圆,则1<t<$\frac{5}{2}$.
其中真命题的序号是( )
①曲线C不可能为圆;
②若1<t<4,则曲线C为椭圆;
③若曲线C为双曲线,则t<1或t>4;
④若曲线C为焦点在x轴上的椭圆,则1<t<$\frac{5}{2}$.
其中真命题的序号是( )
| A. | ③④ | B. | ②③ | C. | ①④ | D. | ①②③④ |
17.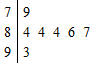 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
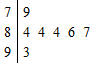 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
