椭圆经过$A$.$B$.则该椭圆的标准方程为$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$．题目和参考答案——青夏教育精英家教网—

题目内容

4．椭圆经过$A（\sqrt{3}，-2）$，$B（-2\sqrt{3}，1）$，则该椭圆的标准方程为$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$．

分析设椭圆的方程为mx²+ny²=1，（m＞0，n＞0．m≠n），把已知点的坐标代入方程，求解方程组得到m，n的值，则椭圆方程可求．

解答解：设椭圆的方程为mx²+ny²=1，（m＞0，n＞0，m≠n），
∵椭圆经过两点$A（\sqrt{3}，-2）$，$B（-2\sqrt{3}，1）$，
∴$\left\{\begin{array}{l}{3m+4n=1}\\{12m+n=1}\end{array}\right.$，解得m=$\frac{1}{15}$，n=$\frac{1}{5}$，
∴椭圆的标准方程为$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$．
故答案为：$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$．

点评本题考查椭圆方程的求法，注意待定系数法的合理运用，是基础题．

练习册系列答案

15．双曲线$\frac{{x}^{2}}{4}$-y²=1的实轴长是4，离心率的值是$\frac{\sqrt{5}}{2}$，焦点到渐近线的距离是1．

12．设函数f（x）=|x|x+bx+c，给出下列4个命题：
①b=0，c＞0时，方程f（x）=0只有一个实数根；
②c=0时，y=f（x）是奇函数；
③y=f（x）的图象关于点（0，c）对称；
④方程f（x）=0至多有2个不相等的实数根．
上述命题中的所有正确命题的序号是①②③．

19．设命题p：?x∈R，x²+x＞a，命题q：?x∈R，使x²+2ax+2-a=0
（1）写出两个命题的否定形式￢p和￢q；
（2）若命题（￢p）∨q为假命题，求实数a的取值范围．

9．已知：全集U=R，集合A={x|4^x＞2}，集合$B=\left\{{\left.x\right|}\right.\left.{\frac{x}{x+2}＜0}\right\}$
（1）求A，B
（2）若M∪（A∪B）=R，且M∩（A∪B）=∅，求集合M．

16．已知命题P：?x∈[1，2]，x²-2x-1＞0，则P的否定是（　　）

	A．	^￢P：?x∈（-∞，1）∪（2，+∞），x²-2x-1＞0		B．	^￢P：?x∈[1，2]，x²-2x-1＞0
	C．	^￢P：?x∈（-∞，1）∪（2，+∞），x²-2x-1≤0		D．	^￢P：?x∈[1，2]，x²-2x-1≤0

13．设函数f（x）=1+（a+1）x-x²-x³
（1）a=0时，讨论f（x）在其R上的单调性．
（2）a=0时，写出f（x）在x=0处切线l的方程
（3）若a＞0，0≤x≤1，求f（x）取得最大值时的x的值．

14．

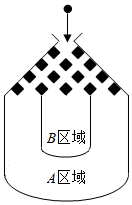如图，将一个半径适当的小球放入容器上方的入口处，小球自由下落，小球在下落的过程中，将遇到黑色障碍物3次，最后落入A区域或B区域中，已知小球每次遇到障碍物时，向左、右两边下落的概率都是$\frac{1}{2}$．
（1）分别求出小球落入A区域和B区域中的概率；
（2）若在容器入口处依次放入3个小球，记X为落入B区域中的小球个数，求X的分布列和数学期望．

试题分类