题目内容
设随机变量ξ服从正态分布N(2,σ 2),则方程x2+4x+2ξ=0无实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:正态分布曲线的特点及曲线所表示的意义
专题:计算题,概率与统计
分析:方程x2+4x+2ξ=0无实数根,可得ξ>2,根据随机变量ξ服从正态分布N(2,σ2),可得曲线关于直线x=2对称,从而可得结论.
解答:
解:∵方程x2+4x+2ξ=0无实数根,
∴△=16-8ξ<0,∴ξ>2.
∵随机变量ξ服从正态分布N(2,σ2),
∴曲线关于直线x=2对称
∴P(ξ>2)=
故选A.
∴△=16-8ξ<0,∴ξ>2.
∵随机变量ξ服从正态分布N(2,σ2),
∴曲线关于直线x=2对称
∴P(ξ>2)=
| 1 |
| 2 |
故选A.
点评:本题考查方程x2+4x+2ξ=0无实数根,考查正态分布曲线的对称性,属于中档题.

练习册系列答案
相关题目
6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为( )
| A、720 | B、144 |
| C、576 | D、684 |
已知复数z满足|z-i-1|+|z+i-1|=2,则z在复平面内对应的点的轨迹是( )
| A、线段 | B、圆 | C、椭圆 | D、抛物线 |
已知y=f(x)是R上的增函数,令F(x)=f(1-x)-f(3+x),则F(x)是R上的( )
| A、增函数 | B、减函数 |
| C、先增后减 | D、先减后增 |
将最小正周期为3π的函数f(x)=cos(ωx+φ)-sin(ωx+φ)(ω>0,|φ|<
)的图象向左平移
个单位,得到偶函数图象,则满足题意的φ的一个可能值为( )
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
已知双曲线的离心率为2,焦点是(6,0),(-6,0),则双曲线的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}中,an=(-1)nn,则a1+a2+…+a10=( )
| A、10 | B、-10 | C、5 | D、-5 |
用数学归纳法证明:1+
+
+…+
=
时,由n=k到n=k+1左边需要添加的项是( )
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+…+n |
| 2n |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
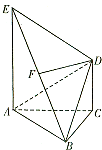 如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.
如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.