题目内容
若直线l1:
(t为参数)与直线l2:
(s为参数)垂直,则k= .
|
|
考点:直线的参数方程
专题:坐标系和参数方程
分析:把参数方程化为直角坐标方程,再根据两条直线垂直的性质求得k的值.
解答:
解:直线l1:
(t为参数)即 y=-
x+2+
,直线l2:
(s为参数)即 y=-2x+1,
再根据这两条直线垂直可得-
•(-2)=-1,求得k=-1,
故答案为:-1.
|
| k |
| 2 |
| k |
| 2 |
|
再根据这两条直线垂直可得-
| k |
| 2 |
故答案为:-1.
点评:本题主要考查把参数方程化为直角坐标方程的方法,两条直线垂直的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A(x-2,
)、B(0,
)、C(x,y),若
⊥
,则动点C的轨迹方程为( )
| y |
| 2 |
| y |
| 2 |
| AC |
| BC |
| A、y2=8x |
| B、y2=-8x |
| C、y2=8(x-2) |
| D、y2=-8(x-2) |
 如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )
如图目标函数z=ax-y的可行域为四边形OAPB(含边界),若P(2,2)是该目标函数z=ax-y的唯一最优解,则实数a的取值范围是( )| A、(-2,-1) | ||
B、[
| ||
C、[-1,-
| ||
D、(-1,-
|
 已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).
已知三角形△ABC的三个顶点分别为A(-1,0),B(1,0),C(0,1).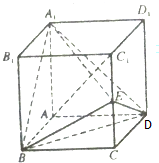 如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.
如图,在正方体ABCD-A1B1C1D1中,点E在棱CC1上.


